GPU-Accelerated Multiple Observer Siting
Wenli Li, W. Randolph Franklin, Salles Viana Gomes de Magalhães, and Marcus V. A. Andrade
Abstract
We present two fast parallel implementations of the Franklin-
Vogt multiple observer siting algorithm, using either OpenMP
or CUDA. In this problem, the objective is to site observers
on a raster terrain such that the joint area visible by them is
maximized. On a portion of terrain with 16,385×16,385 cells,
assuming that observers can see out to a radius-of-interest of
100 cells, finding the approximate 15,000 observers that have
the greatest coverage takes only 17s in CUDA. That is a fac-
tor of 70 speedup from the sequential version. The OpenMP
version exhibits a factor of 17 speedup on a 16 core system.
Applications for the multiple observer siting problem include
radio transmission towers, environmental monitoring sites,
and path planning for surveillance drones. The algorithm has
four steps: finding the visibility indices of all points, selecting
a candidate subset of potential top observers, finding each
one’s viewshed, and greedily constructing the final solution.
Introduction
The purpose of multiple observer siting (Franklin,
et al
. 2002)
is to place observers to cover the surface of a terrain or of
targets above the terrain. It is useful in the placement of radio
transmission towers, mobile ad hoc networks, and environ-
mental monitoring sites.
As described in (Magalhães,
et al
., 2010), an
observer
is a
point in space from which we wish to see or communicate
with other points, called
targets
. The usual notation for ob-
server and target is
O
and
T
. Both the observer and the targets
are considered to be at some given height above the ground
(useful for modeling, e.g., towers). The base points of
O
and
T
are the points on the terrain directly below
O
and
T
, respec-
tively.
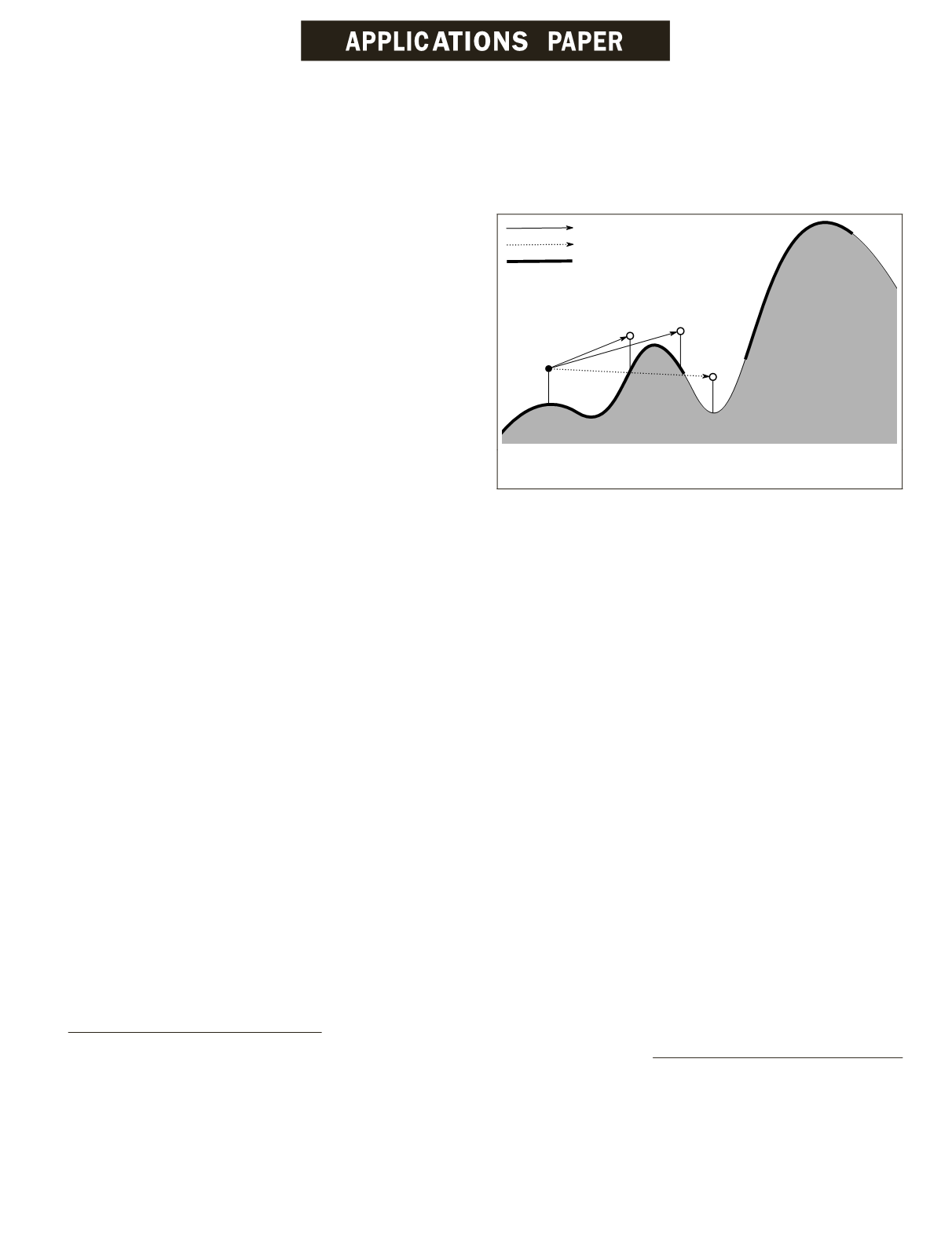
An observer
covers
(or views) a target that is within a given
distance (called
radius of interest
), and that have a direct
line of sight (
LOS
) from the observer. Figure 1 illustrates these
concepts using a section of a terrain model.
The
viewshed V
of an observer
O
is the set of all terrain
points (base points) where targets positioned on these points
are visible from
O
. The
visible area
of an observer is the size
of its viewshed.
The
joint viewshed
of a set of terrain points is the union
of the individual viewsheds of observers sited above these
points. Similarly, the
joint visible area
(or simply
visible area
)
of a set of terrain points is the size of its joint viewshed.
Given a terrain represented as a digital elevation matrix
(
DEM
), there are many choices of what to optimize with the
observer siting. For example, the objective may be to select a
fixed number of observers whose visible area is maximized.
Alternatively, the problem may be to select as few points as
possible such that their visible area is at least a given thresh-
old value.
Other variations of the problem include: using observers
that can cover targets with a quality or probability (Akbarza-
deh,
et al
., 2013), adding constraints such as intervisibility,
where observers are required to be visible from other observ-
ers, using mobile observers and targets (Efrat,
et al
., 2012),
and having different costs for placing observers at different
positions.
The terrain may be either the traditional surface of the
earth, or the tops of buildings in an urban terrain. The observ-
ers may be in remotely operated or autonomous airborne
vehicles, whose operators desire to optimize the flight path.
This may require repeatedly re-computing the siting problem
with slightly varying parameters.
A recent application requiring optimizing observer siting
is
Li-Fi
, or
light fidelity
, which switches LEDs on and off at a
high speed to effect high speed communication. Its main ad-
vantage is its immunity to electronic interference. Its visibil-
ity computation is complicated by its light’s ability to reflect
from shiny surfaces.
“Visibility” is also applicable to
GHz
radio signals that can
be blocked by heavy objects such as reinforced concrete pil-
lars. That is relevant to siting the thousands of beacons that
may be required for indoor way-finding in large buildings
such as airports. For example, Schipol airport’s way-finding
system has 2000 beacons.
Other notable related research includes the many line-
of-sight issues in the Modeling and Simulation community
discussed (with comparisons of various
LOS
algorithms) (Line-
Of-Sight Technical Group, 2004), the relation of visibility to
topographic features (Lee, 1992), and the pioneering work of
(Nagy, 1994). (Champion,
et al
., 2002) studied line-of-sight on
natural terrain defined by an L
1
-spline.
Multiple observer siting is a compute-intensive problem
with considerable inherent parallelism. That, plus the recent
Wenli Li and W. Randolph Franklin are with Rensselaer
Polytechnic Institute, Troy, New York (
.
Salles Viana Gomes de Magalhães is with Rensselaer
Polytechnic Institute, Troy, New York, and the University
Federal de Viçosa, Viçosa, MG, Brazil.
Marcus V. A. Andrade is with Federal de Viçosa,
Viçosa, MG, Brazil.
Photogrammetric Engineering & Remote Sensing
Vol. 83, No. 6, June 2017, pp. 439–446.
0099-1112/17/439–446
© 2017 American Society for Photogrammetry
and Remote Sensing
doi: 10.14358/PERS.83.6.439
Figure 1. Visibility of targets from observers (adapted from
(Magalhães, S.V.,
et al
., 2010)).
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
June 2017
439


