X
Y
Z
X
Y
Z
R
u
v
w
,
A
A
A
S
S
S
=
⋅
+
(1)
where (
X
j
S
,
Y
j
S
,
Z
j
S
) are the linear
EO
elements of scanning line
j
; and (
a
i
,
b
i
,
c
i
),
i
= 1, 2, 3 are the elements in the rotation ma-
trix, which is constructed by angular
EO
elements (
φ
,
ω
,
κ
).
Model (1) is a set of nonlinear equations, where
(
X
A
,
Y
A
,
Z
A
)
are the
GNSS
actual observations, and (
u, v, w
) are
the unknown
GNSS
lever arms. If we know the initial values of
(
u, v, w
), then model (1) can be linearized into the following
form:
v
v
v
X
Y
Z
A
κ
X
Y
Z
S
S
S
A
A
A
=
+ ⋅
∆
∆
∆
∆
∆
∆
ω
φ
+ ⋅
−
R
u
v
w
X
Y
Z
-
X
Y
Z
A
A
A
A
A
A
∆
∆
∆
0
,
(2)
where
A
is the coefficient matrix for unknowns
(
Δ
ω
,
Δ
φ
,
Δ
κ
) and the initial values (
X
A
,
Y
A
,
Z
A
) are approxi-
mated according to model (1). The other symbols are listed in
Table 1.
For
GPS
-assisted frame cameras such as the Wild-RC20,
DMC
, and
UCD
, the
GPS
observation model can be constructed
according to Equation 2. However, the processing for the
GFXJ
camera is more complicated. For linear
CCD
images, each im-
age line has an independent perspective center, and the
EO
elements for each scan line are different from each other. For
example, the imaging frequency of the
DMC
is 2 s per frame
and that of the
GFXJ
is 1080
Hz
, so the number of unknown
EO
elements for the
GFXJ
camera is far more than that for the
frame camera. The correlation among
EO
elements poses
a challenge to the stability and reliability of
AT
(Kocaman
2003, 2008; Jama 2011). In model (2), the unknown
EO
ele-
ments and
GNSS
lever arms are solved together in a combined
triangulation procedure (Kocaman 2006, 2008).
In theory, the combined triangulation procedure is very
rigorous. However, practical research on the
GFXJ
camera
confirmed that the integral model could not obtain stable and
reliable calibration values for
GNSS
lever arms due to the cor-
relation among
EO
elements and
GNSS
lever arms. Thus, in this
paper, we propose and set up the following
GNSS
lever arms
calibration model:
v
v
v
R
u
v
w
X
Y
Z
-
X
Y
Z
A
A
A
A
A
A
= ⋅
-
∆
∆
∆
X
Y
Z
,
A
A
A
0
(3)
where the meaning of each parameter remains unchanged
from model (2). However, model (3) is more appropriate
for the
GNSS
lever arms calibration.
EO
elements are solved
through
AT
and remain constant during the calibration pro-
cess based on model (3). In the
GNSS
lever arms calibration,
only (
Δ
u
,
Δ
v
,
Δ
w
), the
GNSS
lever arms, are treated as un-
knowns. If the
GNSS
lever arms have been accurately mea-
sured prior to flight and are taken into account in the
GNSS
observations, the calibration values (
Δ
u
,
Δ
v
,
Δ
w
) are the differ-
ences between the actual
GNSS
lever arms and the laboratory
measured values. The larger the topographic mapping scale is,
the more that minor differences in the
GNSS
lever arms caused
by various flight conditions should be considered.
IMU Boresight Misalignment Calibration of the GFXJ camera
The
GNSS
/
IMU
system provides information about the
IMU
’s
position, attitude, speed, and acceleration in the ground
coordinate system. However, what the
AT
process needs is
the position and attitudes of the camera center in the ground
coordinate system. In practice, the
IMU
is rigidly connected to
the aerial camera and keeps the corresponding axes paral-
lel as much as possible. The relative relationship between
the
IMU
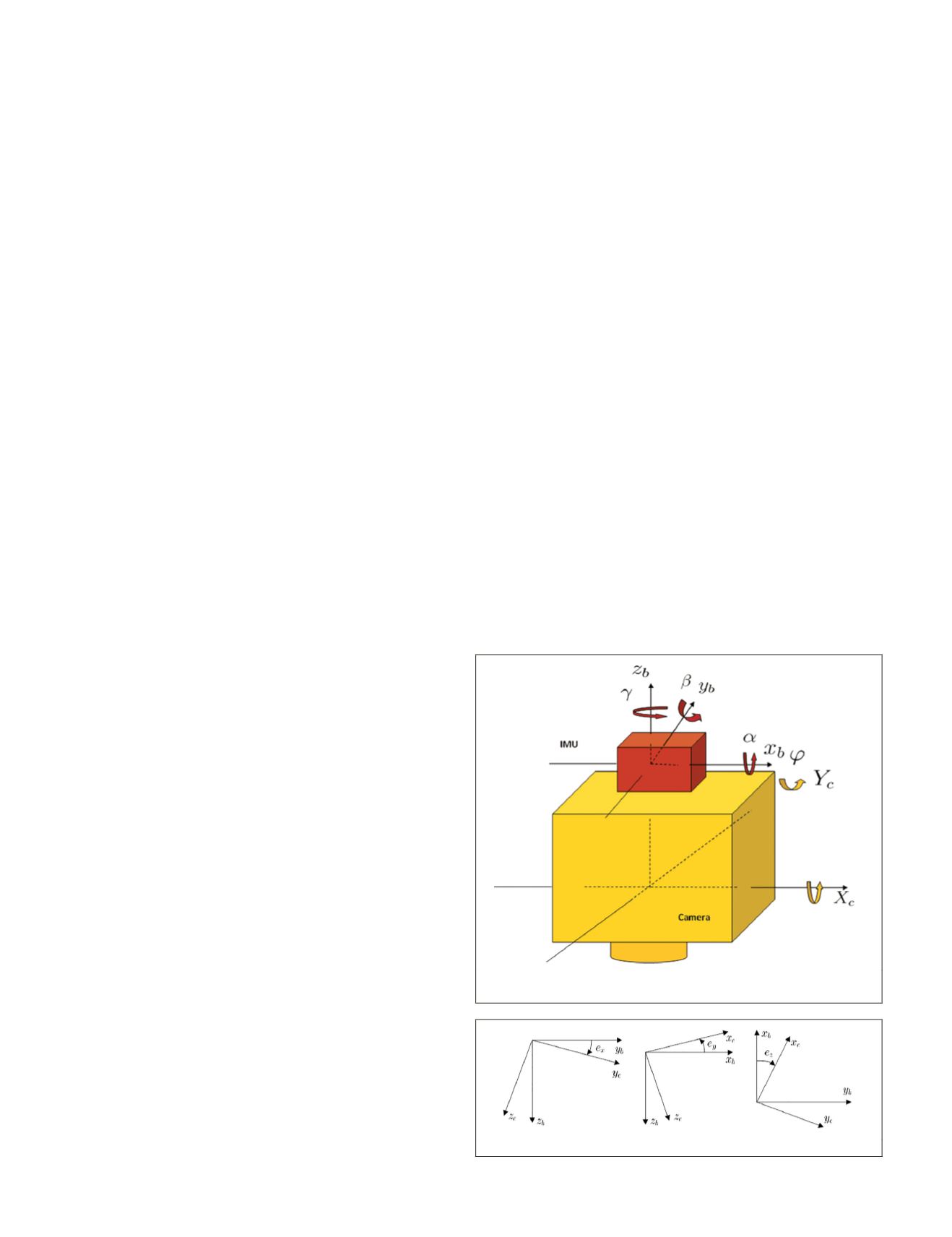
equipment and camera is shown in Figure 4, where
the subscript “b” represents the
IMU
and the subscript “c”
represents the camera. Due to installation reasons, it is almost
impossible for the corresponding axes of the
IMU
and the cam-
era to be strictly parallel. An angular difference always exists
between the corresponding axes, and this difference is called
the
IMU
boresight misalignment.
The
IMU
boresight misalignment can be decomposed into
angle deviations in three respective directions
e
x
,
e
y
,
e
z
, as
shown in Figure 5. Typically, the values of
IMU
boresight
misalignment are small (< 3°). However, in special installa-
tions, the values may be ±
π
/2. Since the
IMU
axes are not vis-
ible and the
IMU
, which is mounted inside the camera itself,
is sometimes not visible, it is difficult to measure the
IMU
boresight misalignment directly. However, the
IMU
boresight
misalignment seriously affects the camera georeferencing ac-
curacy, so this misalignment must be calibrated in practical
applications.
The
IMU
observations (
α
,
β
,
γ
) form the rotation matrix
R
b
m
,
the
EO
angular elements (
ω
,
φ
,
κ
) form the rotation matrix
R
c
m
,
and the
IMU
boresight misalignments (
e
x
,
e
y
,
e
z
) form the rota-
tion matrix
R
b
c
.
R
r r r
r r r
r r r
R
a a a
b b b
c
b
m
c
m
=
=
11 12 13
21 22 23
31 32 33
1 2 3
1 2 3
1 2 3
11 12 13
21 22 23
31 32 33
=
c c
R
e e e
e e e
e e e
c
b
Figure 4. Relative geometric relationship between the
IMU
and camera.
Figure 5. Boresight misalignments between the
IMU
and camera.
646
September 2019
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


