The transformation from image coordinates into object space
coordinates is usually done using the following equation:
x
y
c
a a a
a a a
a a a
X X
O
−
=
−
λ
11 12 13
21 22 23
31 32 33
•
Y Y
Z Z
,
O
O
−
−
…
(2)
Where:
x– , y– are image coordinates of points,
X,Y,Z are object-space coordinates of points,
X
O
,Y
O
,Z
O
are the object-space coordinates of exposure sta-
tions,
C is the camera constant,
λ
is a scale factor, and
a
ij
are the coefficients of transformation
Equation (2) may be expressed as:
x c
a X X a Y Y a Z Z
a X X a Y Y a Z Z
O
O
O
O
O
+
−
(
)
+ −
(
)
+ −
(
)
−
(
)
+ −
(
)
+ −
11
12
13
31
32
33
O
O
O
O
O
O
and
y c
a X X a Y Y a Z Z
a X X a Y Y
(
)
=
+
−
(
)
+ −
(
)
+ −
(
)
−
(
)
+ −
0,
21
22
23
31
32
(
)
+ −
(
)
=
a Z Z
.
O
33
0
(3)
Substituting equation (1) into equation (3) one gets:
a a x a y c
a X X a Y Y a Z Z
a X X a Y Y
O
O
O
O
O
1 2
3
11
12
13
31
32
+ + +
−
(
)
+ −
(
)
+ −
(
)
−
(
)
+ −
(
)
+ −
(
)
=
+ + +
−
(
)
+ −
(
)
+ −
a Z Z
,
and
a a x a y c
a X X a Y Y a Z Z
O
O
O
O
33
4 5
6
21
22
23
0
(
)
−
(
)
+ −
(
)
+ −
(
)
=
a X X a Y Y a Z Z
.
O
O
O
31
32
33
0
(4)
Eliminating y from equations (4), one gets:
a a a a a a a a x
c
a a a a X X a a a a
1 6
6
1 6
O 1 6
−
(
)
+ −
(
)
+
−
(
)
−
(
)
+ −
(
4 3
2
5 3
1
3 21
2
22 3
)
−
(
)
+ −
(
)
−
(
)
−
(
)
+ −
(
)
+ −
(
)
=
Y Y a a a a Z Z
a X X a Y Y a Y Y
O 1 6
O
O
O
O
3
23 3
31
32
33
0.
(5a)
Eliminating x from equations (4) one gets:
a a a a a a a a y
c
a a a a X X a a a a
1
1
O 1
5 4 2
3 5 6 6
1 5 21 2
2 5 22 2
−
(
)
+ −
(
)
+
−
(
)
−
(
)
+ −
(
)
−
(
)
+ −
(
)
−
(
)
−
(
)
+ −
(
)
+ −
(
)
=
Y Y a a a a Z Z
a X X a Y Y a Y Y
O 1
O
O
O
O
3 5 23 2
31
32
33
0.
(5b)
Equations (5a) and (5b) may be expressed as:
d d x
b X b Y b Z b
b X b Y b Z b
,
and
d d x
b X b Y b
1 2
1
2
3
4
9
10
11
12
3 4
5
6
0
+
+ + +
+ + +
=
+
+ +
7
8
9
10
11
12
0
Z b
b X b Y b Z b
.
+
+ + +
=
(6)
Eliminating d
1
and d
3
from equations (6) one gets:
d x
b X b Y b Z b
b X b Y b Z b
,
and
d y
b X
2
1
2
3
4
9
10
11
12
4
5
0
+
+ + +
+ + +
=
+
+
′
′
′
′
′
′
′
′
′
b Y b Z b
b X b Y b Z b
.
′
′
′
′
′
′
′
+ +
+ + +
=
6
9
8
9
10
11
12
0
(7)
Eliminating d
2
and d
4
from equations (7), one gets:
x
b X b Y b Z b
b X b Y b Z b
,
and
y
b X b Y
*
*
*
*
*
*
+
+ + +
+ + +
=
+
+
′
′
′
′
1
2
3
4
9
10
11
12
5
6
0
+ +
+ + +
=
′
′
′
′
b Z b
b X b Y b Z b
.
*
*
7
8
9
10
11
12
0
(8)
Eliminating b
12
′
from equations (8), one gets:
l
1
X +
l
2
Y +
l
3
Z +
l
4
l
9
X +
l
10
Y +
l
11
Z + 1
x + =0,
and
(9)
l
5
X +
l
6
Y +
l
7
Z +
l
8
l
9
X +
l
10
Y +
l
11
Z + 1
y + =0.
Equations (9) are the basis of the proposed method.
3. Mathematical Model in the Conventional (Collinearity)
Approach
As mentioned above, the transformation from comparator co-
ordinates (x, y) into image coordinates (x– , y– ) is usually done
using equations (1):
x– = a
1
+ a
2
x + a
3
y
(1)
y– = a
4
+ a
5
x + a
6
y
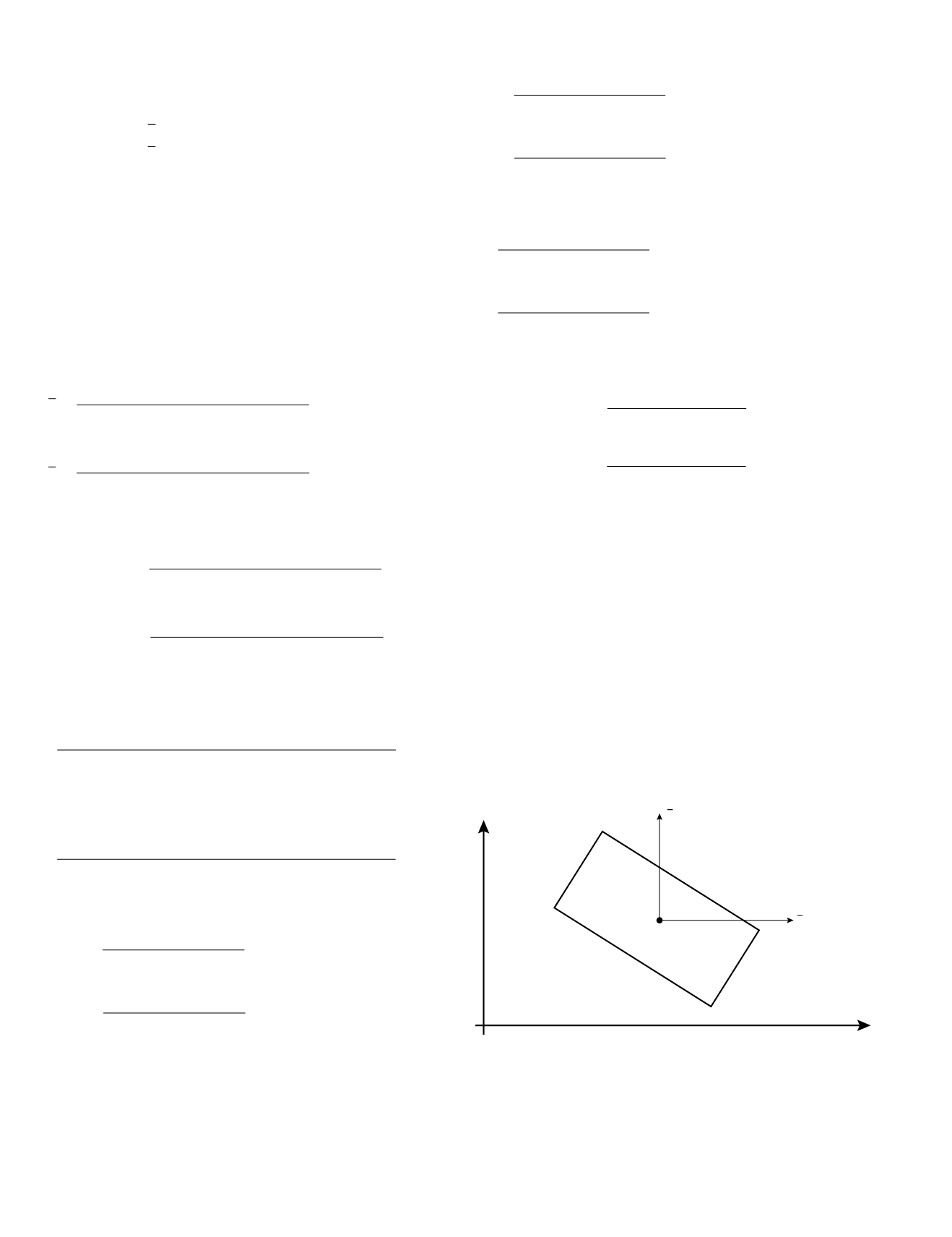
Since the selection of the image coordinate axes is ar-
bitrary, let us select the definition shown in Fig. 1, where
the y– image coordinate axis is parallel to the y comparator
coordinate axis and passes through the image principal point
(0). The x– image coordinate axis is perpendicular to the y– axis
and intersects it at the image principal point.
x
y
y
0
x
Figure 1. Coordinated Axes. (x & y: comparator coordinate aces; x– &
y– : image coordinate axes).
104
February 2015
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


