2007; Sathymoorthy
et al
., 2007). Naturally,
MM
is widely
applied to extract buildings (Rottensteiner
et al
., 2002; Brunn
et al
., 1997; Zhan
et al
., 2002; Sportouche
et al
., 2011). Zhan
et al
. (2002) proposed a volumetric approach, where the
DSM
was considered in multiple layers, i.e., slices. The connected
component in each slice was labeled. Such a component was
classified as belonging to a building if the components in the
vertically neighbored slices had similar sizes and centers of
gravity. Rottensteiner
et al
. (2002) extracted initial building
masks using a binary segmentation based on a height thresh-
old. Then, they used the binary morphological opening to
separate and filter out small thin objects and analyzed the
DSM
textures to eliminate vegetation and other areas. The final
individual building regions were determined using a connect-
ed component analysis, where a decreasing-sized structural
element for morphological opening helped to split the regions
that corresponded to more than one roof plane. Brunn
et al
.
(1997) used a binary classification to distinguish vegetation
from buildings, by applying morphology to derive closed ar-
eas on the surface normal variance and select valid vegetation
segments. Li
et al
. (2014) used a modified white top-hat trans-
form with directional edge constraints to filter airborne lidar
data and extract the ground points and then buildings. Other
studies used
MM
on a multi-spectral image instead of
DSM
,
and produced good results. Lefevre (2007) used very high-
resolution (
VHR
) gray level images as the input data to extract
the buildings. They transformed the image to a binary image
where the bright or dark buildings can be separated from the
others. Then, a morphological filter was applied to remove
the objects that are smaller than a given minimal size of a
building. Huang (2011) proposed a morphological building
index (
MBI
) to represent the brightness, size, and orientation
of the buildings using the reconstruction, differential morpho-
logical profile (
DMP
), and directionality. However, the
MBI
fea-
ture image needs to be segmented according to a threshold to
extract the buildings, which is neither flexible nor adaptable.
Besides,
DMP
cannot reflect the height characteristics, but only
the size of the building. Meng (2012) proposed a method for
detecting the residential land use of buildings from lidar data,
aerial photography, and road maps using a morphology-based
building detection algorithm. The decision tree analysis was
used to distinguish single family residential from multi-fami-
ly residential buildings.
To summarize, the above algorithms and methods gener-
ally employ lidar data for building extraction, because it is
more accurate than photogrammetry-derived
DSM
data in
terms of direction and height. However, one of the advantages
of a
DSM
is that it can be simply and economically derived
from photogrammetry, so it is a practical choice for building
extraction and modeling. The purpose of our research is to
find a proper method to extract the separated houses in dense
residential areas using
DSM
. To this end, we propose an
MM
-
based building scale detection method and a reconstruction
method to create a mask for a building and furthermore to
obtain its footprint.
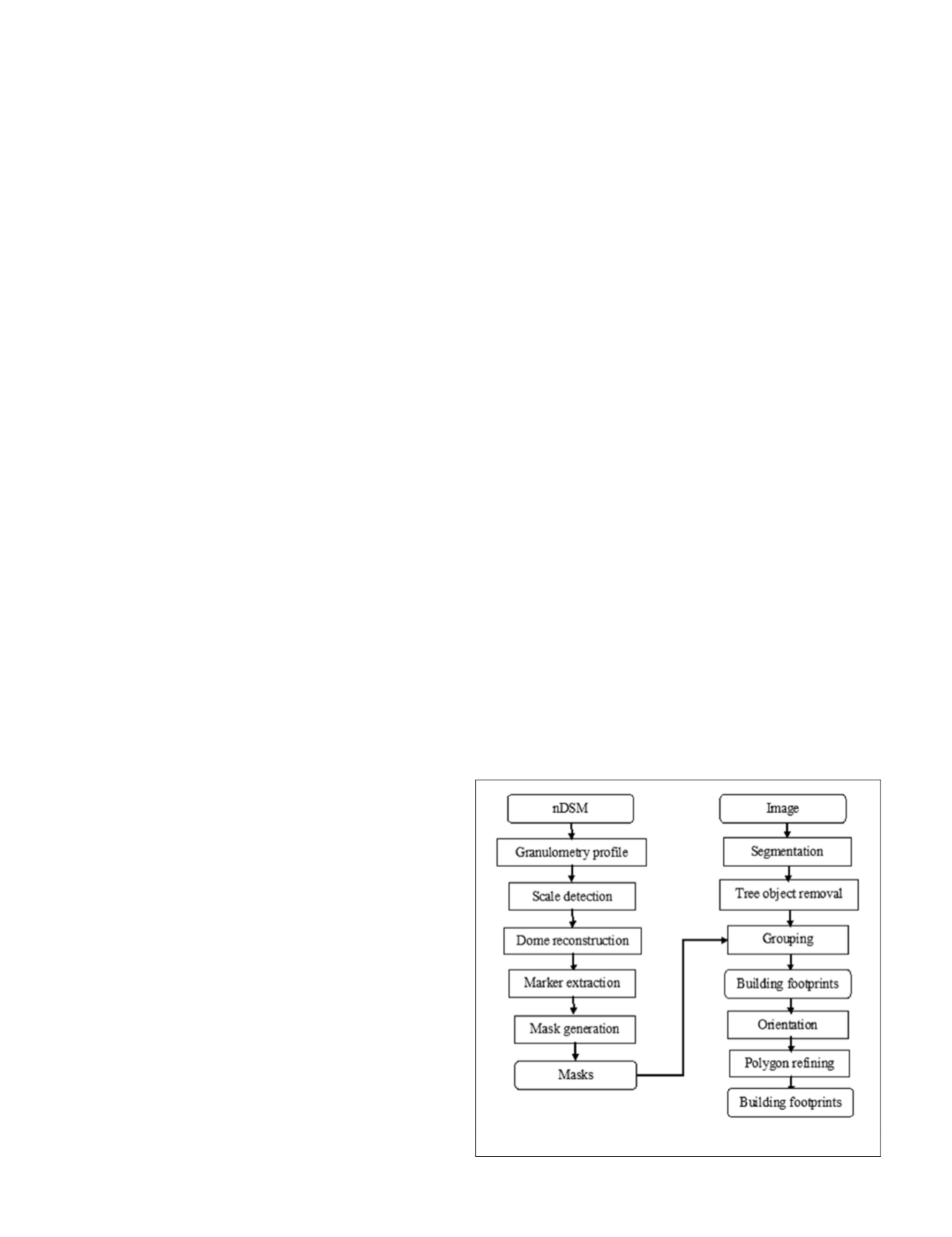
The Proposed Technique
The proposed technique can be described by the flow diagram
shown in Figure 1. It is composed of three main stages. The
first stage is finding the scales of the buildings in the scene by
granulometry analysis of normalized
DSM
(
nDSM
). A morpho-
logical algorithm similar with multiple morphological build-
ing index (
MBI
) (Huang
et al
., 2011) is proposed to do this.
The second stage is reconstructing and extracting the ideal
domes of the small houses according to the detected scales.
A set of associated processing is developed. The third stage
is extracting and modeling the houses from the image on the
basis of the masks.
Morphological Transformations for DSM
The gray level (
GL
) image/
DSM
can be considered as a collec-
tion of level images, each corresponding to a horizontal slice
of the
DSM
when viewing the
DSM
as a surface. The inner pixel
has a value of 1, the outer pixel has a value of 0. Morphologi-
cal operations output the sum of all the results when applying
to all the levels. Vincent and Pierre (1991) stated that an
open-
ing
removed some peaks and crest lines, whereas a
closing
tended to fill in basins and valleys (Vincent
et al.
, 1991).
Reconstruction
Morphological reconstruction can be used to isolate certain
features in an image, based on the manipulation of a mask
image
f
and a marker image
g
(Sathymoorthy
et al.
, 2007). It is
founded on the concept of performing
geodesic dilation
s of a
marker image until achieving stability (represented by a mask
image). The elementary
geodesic dilation
(Vincent, 1993;
Pesaresi
et al.
, 2001) is defined as:
δ
f
(1)
(
g
) = (
g
5
B
)
∧
f
(1)
where
5
denotes standard
dilation
, and
∧
represents the
pointwise minimum. The
n
-times of
geodesic dilation
is:
δ
f
(
n
)
(
g
) =
δ
f
(1)
%
δ
f
(1)
%
…
%
δ
f
(1)
(
g
).
(2)
This leads to a definition of the
reconstruction
of
f
from
g
:
ρ
f
(
g
) =
∨
≥
n
1
δ
f
(
n
)
(
g
).
(3)
where
∨
represents the pointwise maximum.
Regional Maximum
A regional maximum (M) of a
GL
image (I) is a connected
component of pixels with a given value
h
, such that any pixel
in the neighborhood of M has a strictly lower value (Vincent,
1993). A regional maximum of the
DSM
is then a plateau at
altitude
h
. The buildings in the
DSM
are identified as convex
off-terrain objects with certain shapes, if viewing the
DSM
as
a 3
D
surface. So, the direct way to detect the buildings is to
extract these regions; the top part with height
h
. In
MM
, this
is implemented by subtracting
h
from the
GL
image
I
and then
reconstructing the image. That is,
Figure 1. Flow diagram of the proposed method.
22
January 2016
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


