Determination of Criteria Weights
In many applications of multiple criteria aggregation, in addi-
tion to the ordered weights of the criteria (
w
j
), another weight
(
v
j
) is required to reflect the relative significance or the prior-
ity of the criteria. The former term reflects the decision strat-
egy and the latter indicates the criteria preferences regarding
the decision-maker attitude (Nadi and Delavar, 2011).
To combine these two types of weights, Yager (1997) pro-
posed a criteria weight modification approach for generating
the order weight (
w
j
) based on the inclusion of criterion weight
(
v
j
) according to the reordered criterion value as Equation 5:
w
v
v
v
v
j
k
j
k
k
n
k
k
j
k
k
n
k
=
−
=
=
=
−
=
∑
∑
∑
∑
(
) (
)
1
1
1
1
1
α
α
.
(5)
The criteria weights typically have the following property
(Equation 6):
j
n
j
v
=
∑
=
1
1
.
(6)
So, for alternative
i
in the data set the
OWA
operator can be
defined as Equations 7 and 8:
w v
v
j
k
j
k
k
j
k
=
−
=
=
−
∑ ∑
(
) (
)
1
1
1
α
α
(7)
OWA
i
j
n
k
j
k
k
j
k
j
v
v c
=
−
=
=
=
−
∑ ∑ ∑
1
1
1
1
α
α
.
(8)
where
α
indicates the decision strategy based on Equation 4.
In the case of road vectorization, the criteria weights
should be determined considering the relative importance of
the road segment criteria. A simple and reliable method for
estimating criteria weights is based on a ranking of evaluation
criteria according to their preference (Stillwell
et al
., 1981).
Referring to this method, the
j
th
criterion weight can be calcu-
lated as Equation 9:
v
n r
n r
j
j
k
n
k
=
− +
− +
=
∑
1
1
1
(
)
(9)
where
j
is the rank position of the
j
th
preferable criterion. The
most important criterion ranks first (
r
j
= 1
), the second most
important criterion ranks second
(r
j
= 2
), and so on; a rank of
r
j
= n
is assigned to the least important criterion;
n
is the num-
ber of criteria. Referring to Equation 9, the more preferable the
criterion is, the higher weight is assigned.
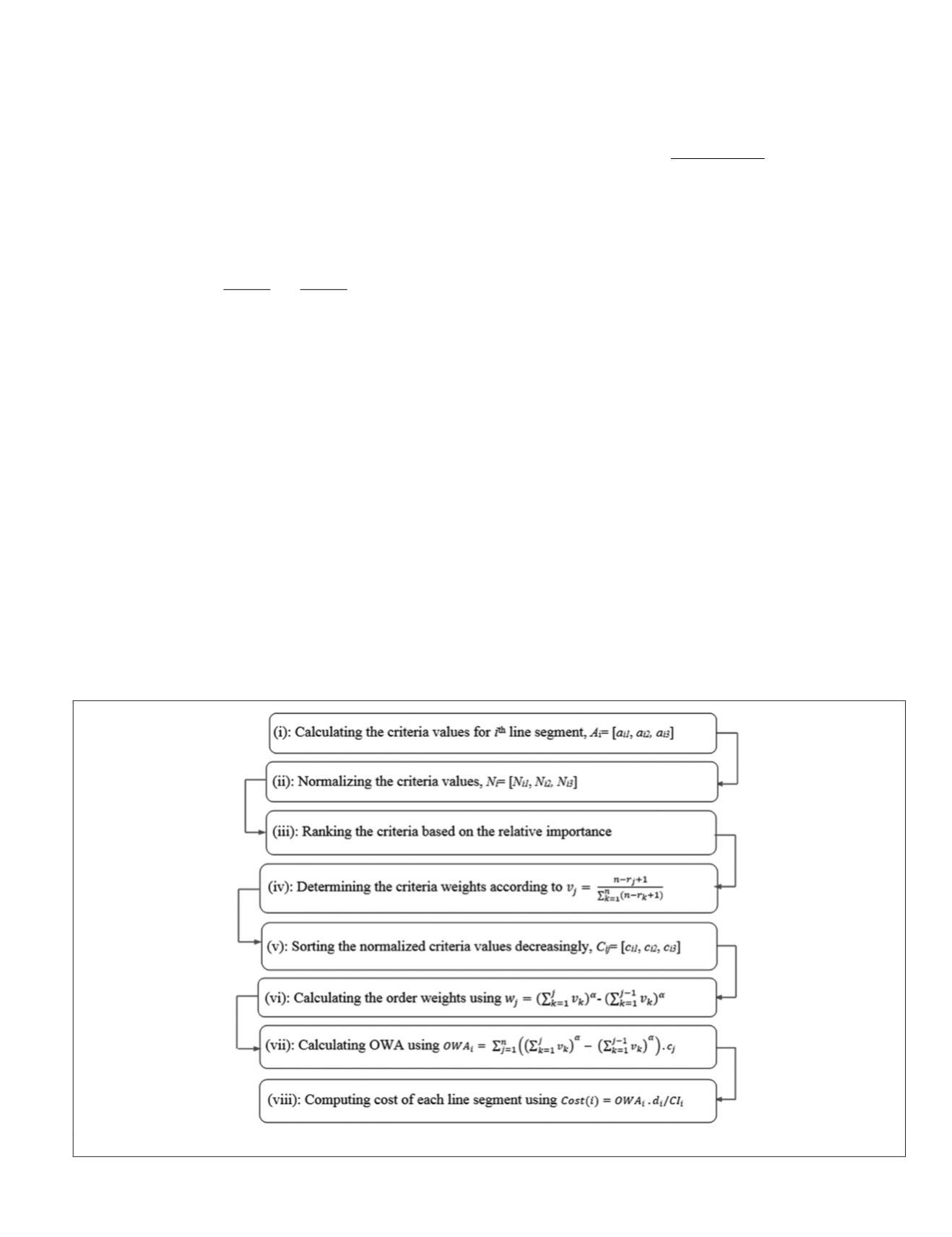
Calculation of Cost for Each Line Segment
Following the determination of normalized criteria values,
criteria weights, and aggregation strategy (ORness value), one
can calculate the overall aggregation value of each alternative
(line segment) utilizing the
OWA
based decision operator. The
OWA
aggregation operators are used to transform the pre-
defined properties (criteria) of road segments into normalized
values in the range of [0,1]. The cost value of
i
th
line segment
is calculated using Equation 10:
Cost
(
i
) =
OWA
i
.
d
i
/
Cl
i
,
(10)
It is obvious in Equation 10, the value of cost is directly
proportional to the length of the line segment. In that, the cost
value is raised by increasing the distance between road key
points. Conversely, the cost value is indirectly proportional
to the
CI
value. By increasing the number of road pixels in the
circular intersection area of corresponding road key points,
the cost value is decreased which leads to selection of the
assumed line segment as a road segment. On the whole, this
cost function is a decision criterion to accept a line segment
as a road segment or reject it. The procedure of cost calcula-
tion for each line segment is summarized in Figure 5.
Figure 5. Computing cost of
i
th
line segment based on OWA.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
February 2016
111


