different corners of the L0 image are first backprojected
to the object space with the help of a given elevation
(typically the lowest or average elevation of the ter-
rain), and six affine parameters are then determined
from the linear equations of the 2
D
affine transforma-
tion model.
2. Iterative search
Two important issues in iterative search are the itera-
tive step size and the convergence conditions.
Both the
Δ
x
F
and
D
criteria can be applied in the itera-
tive search, and their corresponding step size equations
are given by:
x
B
b
x
step
F
int
D
=
(5)
and
x
D
d
D
step
=
int
(6)
respectively, where the int function is used to ensure that the
searched scan line is always located at an integer position;
D
is a signed number, and its sign is determined by which
side the ground point is located with respect to the normal
direction of a scan plane;
B
is the distance between the in-
stantaneous perspective centers corresponding to the current
searched and correct scan lines (i.e., the base length between
S and S
ˆ
in Figure 6), and it can be estimated from the geomet-
ric relationship shown in Figure 6 and given by:
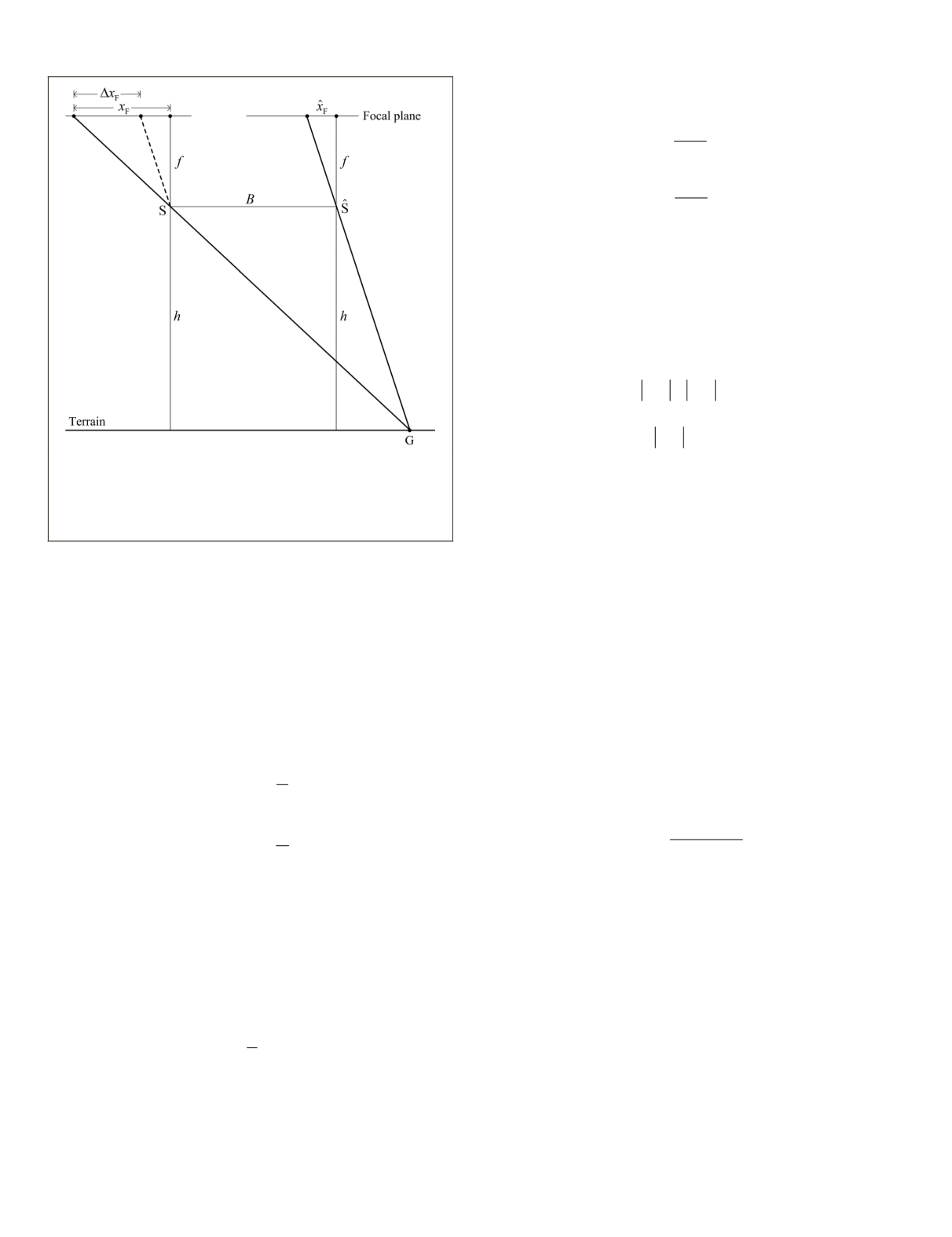
B
h
f
x
= D
F
(7)
where
h
is the flight height above ground.
The symbols
b
and
d
in Equations 5 and 6 refer to the
average base length (i.e., the average distance between the
instantaneous perspective centers corresponding to two
adjacent scan lines) and the average point-plane distance
corresponding to two neighboring scan lines, respectively,
and they are derived by:
b
B
N
N
=
−
−
1
1
(8)
and
d
D
N
N
=
−
−
1
1
(9)
respectively, where
B
N
–1
represents the distance between
the instantaneous perspective centers corresponding to the
first and last scan lines of the L0 image,
D
N
–1
is the distance
between the last perspective center and the first scan plane
(Wang
et al
., 2009), and
N
is the total number of scan lines in
the L0 image.
Whether the
Δ
x
F
criterion or
D
criterion is applied, the two
adopted convergence conditions are:
x x
i
i
step
step
≥
−
1
(10)
and
x
i
step
≤
1
(11)
where the superscript
i
refers to the
i
th
iteration.
3. Sequential search
The scan line determined by the iterative search is al-
ready very close to the correct one, and the discrepancy
is typically within the range of less than one to several
pixels. The following sequential search aims to further re-
duce the discrepancy to be less than or equal to one pixel.
The sequential search only needs to be implemented
at one side of the current scan-line position. If the cor-
responding
Δ
x
F
of the current scan line is a positive
number, the sequential search should be in the forward
direction because
Δ
x
F
is almost a monotonically decreas-
ing function of the scan-line coordinate. In turn, if
Δ
x
F
is
negative, the search should be in the backward direction.
The sequential search stops when it satisfies
D D
x x
n
n
F
F
⋅
≤
+
1
0
(12)
4. Interpolation
Finally, a linear interpolation is applied to achieve a
sub-pixel accuracy for the scan-line coordinate.
x x
x
x x
n
n
n
n
= +
−
+
D
D D
F
F
F
1
(13)
where
x
n
is the integer-pixel coordinate obtained from
the sequential search.
Experiments
Data Description
Eighty-five flight strips, which were captured by three differ-
ent Leica
ADS
80 scanners, and in various flight conditions,
were selected for the test, and each strip contained three
panchromatic images with different views (i.e., backward,
nadir, and forward). Table 1 lists the technical parameters of
two selected strips.
Strategy
The experimental procedures were similar to those of Wang
et
al
. (2009). Real trajectories and camera calibration parameters
were used, but the ground points were derived from a simula-
tion in order to better cover the whole image (not including the
Figure 6. The relationship between the focal-coordinate differ-
ence
Δ
x
F
and the base length
B
in a vertical imaging condition.
S
and
S
ˆ
are the instantaneous perspective centers correspond-
ing to the current searched and correct scan-line coordinates,
respectively.
568
July 2015
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


