triangle differs as a result of the spatial distribution and
density of points: the triangles are small on the surface of
the trunk/branches where the point density is high, but large
when noise points are present, especially in the leaf part of
the tree. For the purpose of excluding noise points, the raw
points in each sliced bin were filtered by triangle size: only
the vertices of triangles with areas smaller than 3.0 × 3.0 mm
2
were kept. As shown in Figure 3, noise points were filtered
and those surrounding the circle were retained after filtering.
Note that the TIN filter was not applied to the virtual tree,
because our simulation is free of noise points.
Step 3 - Detecting Circles and Lines
The detection of geometric primitives such as circles, circle-
like shapes, and line segments enables trees to be simplified
to skeleton points consisting of circle centers and line nodes.
Previous researchers detected circles using the Hough trans-
form on grayscale images instead of points (Simonse
et al
.,
2003; Schilling
et al
., 2012). Two key parameters are required
for circle detection using the Hough transform: the radius of
the circle to be detected and the minimum number of pixels
that belong to a circle in the image space (Duda and Hart,
1972). In our case, points were processed instead of images,
and the two parameters required by the Hough transform
were not pre-known. In addition to circles, branch slices with
circle-like shapes such as arcs and incomplete circles may
be encountered. We detected circles and circle-like shapes
from unorganized points simultaneously by projecting all the
points within a sliced bin onto the 2
D
x
-
y
plane. Then, based
on the medial axis transform (Verroust and Lazarus, 2000), a
line parallel to the
y
-axis was moved along the
x
-axis, and the
middle position of the points intersecting with the line was
recorded. After line sweeping, the middle points of circles
and circle-like shapes can all be shaped into line segments
(Figure 4). The detection of circles and circle-like shapes
can therefore be replaced by the detection of line segments.
It should be noted that the line-sweeping procedure was
repeated a second time along the
y
-axis to achieve a higher
detection rate (Figure 4).
A modified Hough transform operating directly on
points instead of images was developed for finding straight
line segments (medial axis). If
k
is the slope of the line, and
b
is the
y
-intercept, a straight line can be described as:
y
=
k
·
x
+
b
(1)
In addition to this slope–intercept model of a straight line, the
same straight line can be treated as a dot in the (ρ
, θ
) parameter
space constructed explicitly by the Hough transform:
ρ
= cos
θ
·
x
+ sin
θ
·
y
(2)
where
ρ
represents the algebraic distance between the line
and the origin, and
θ
represents the angle between the vector
from the origin and this closest point. The Hough transform
considers the image in the parameter space, from which lines
are obtained as local maxima in an accumulator consisting
of (
ρ
,
θ
) (Duda and Hart, 1972). In our modified version of the
Hough transform, the pixels in traditional 2D images were
replaced by the middle points found after line sweeping, and
the accumulator array was modified as follows.
1. The array consisted of a cell
ID
and a point counter for
the corresponding
ID
.
2. The cell
ID
equaled the difference between the
y
-values
(assuming the sweeping line moves along the
x
-axis) of
the point being checked and the base point, which had
the lowest
y
-value.
Assuming that the sweeping line moves along the
x-
axis,
for each middle point, the point counter of the corresponding
cell
ID
was incremented by one, so a high count in a given cell
corresponded to a line segment. Adjacent points with slightly
different
y
-values were also treated as being within the same
line segment. This was achieved by incrementing not only
the point counter of the middle point being checked, but also
the point counters of its neighboring middle points within the
range of the specified
y
-value difference. Let
AccumulatorAr-
ray
be the Hough structure composed of
Cell
ID
and
CellCont
.
Let
Middle_points
represent the middle points found by the
sweeping line, and
Tolerance
be the range of the specified
y
-value difference. The pseudo codes for the aforementioned
procedure are as follows:
First, sort
Middle_points
by
y
-axis value;
Second, for (i = 0; i <number of
Middle_points
; i++)
{
Cell
ID
=
Middle_point
[i].
y
-
Middle_poin
t[0].
y
;
for (j = (-1*
Tolerance
);
j
< =
Tolerance
; j++)
{
Cell
ID
=
Cell
ID
+ j;
AccumulatorArray
[
Cell
ID
].
CellCont
=
AccumulatorArray
[
Cell
ID
].
CellCont
+ 1;
AccumulatorArray
[
Cell
ID
].
Cell
ID
=
Cell
ID
;
}
}.
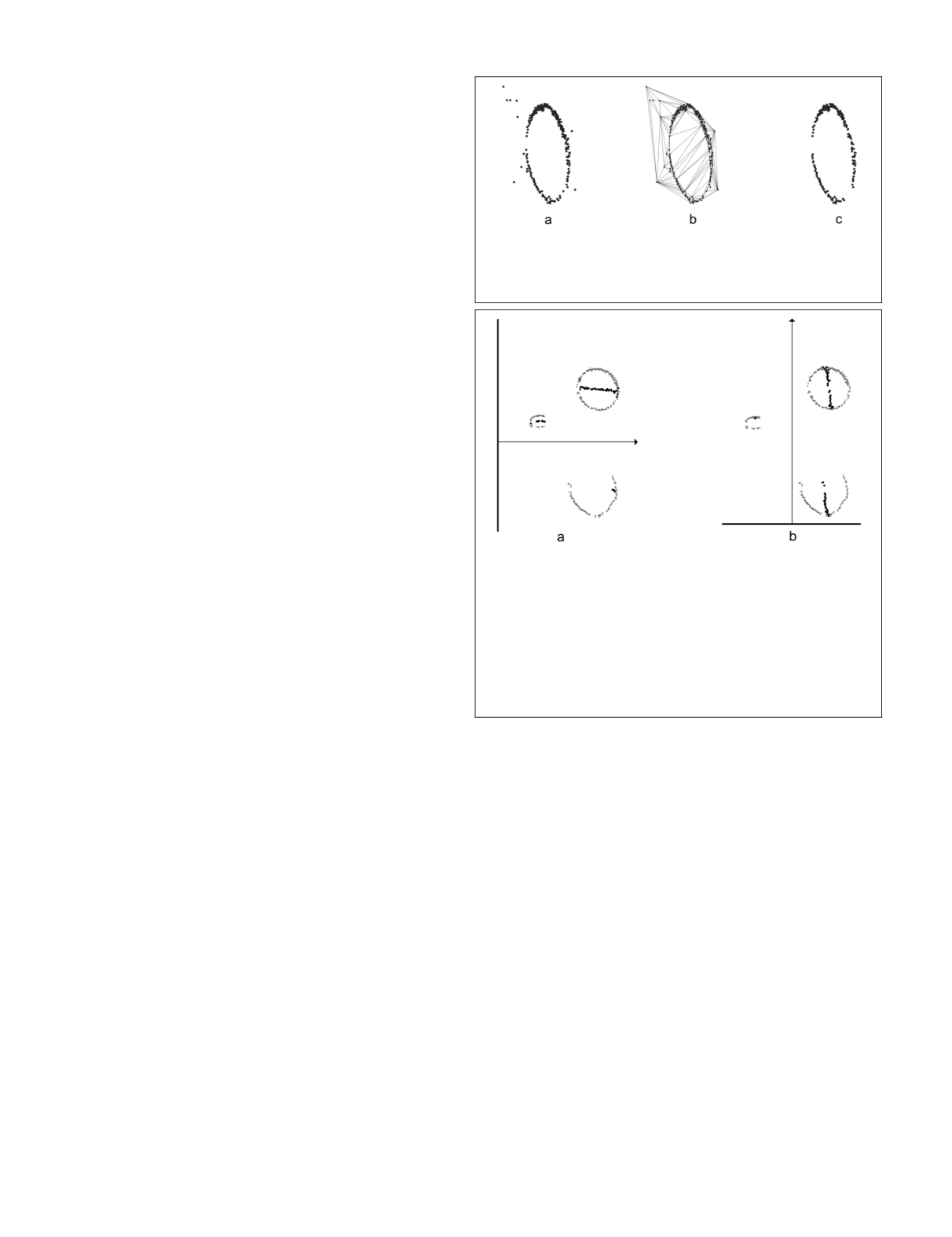
Figure 3. Noise filtering using triangular irregular networks (TINs):
(a) points of sliced bin projected onto 2D plane before TIN filter-
ing, (b) points and TINs, and (c) points of same sliced bin after
TIN filtering.
Figure 4. Sweeping line (indicated by black line) for detecting
circles and circle-like shapes. Black points show the middle
points detected by the sweeping line, and the direction of move-
ment of the sweeping line is indicated by the arrow. After the line
was swept in two directions, all the circles and incomplete circles
were transformed into line segments and then detected using
the modified Hough transform: (a) a sweeping line moving along
the
x
-axis; the incomplete circle at the bottom was not detected
by the sweeping line, and (b) a sweeping line moving along the
y
-axis; the arc on the left was not detected by the sweeping line.
770
October 2015
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


