∆
∆
x x x k r
y y k r
= −
(
)
(
)
= −
(
)
(
)
0
0
y
1
2
1
2
(2)
where,
k
1
represents the first radial distortion coefficient.
r
x x y y
= −
(
)
+ −
(
)
0
2
0
2
is the distortion radius which is the
Euclidean distance of the distorted point to the distortion
center. Therefore, the corresponding undistorted point (
x
– ,
y
– )
can be derived:
x x x x x x x x x k r
y y y y
y y y
− = −
(
)
+ = −
(
)
+ −
(
)
(
)
− = −
(
)
+ = −
(
)
+
0
0
0
0
0
0
0
∆
∆
y
1
2
−
(
)
(
)
y k r
0
1
2
.
(3)
Radial Distortion Correction from Vanishing Points
The intersection of parallel lines in the object space is placed at
infinity, and its projection onto the image space is called vanish-
ing point. But due to the influence of radial distortion, the vanish-
ing point may not be the actual intersection in the image plane.
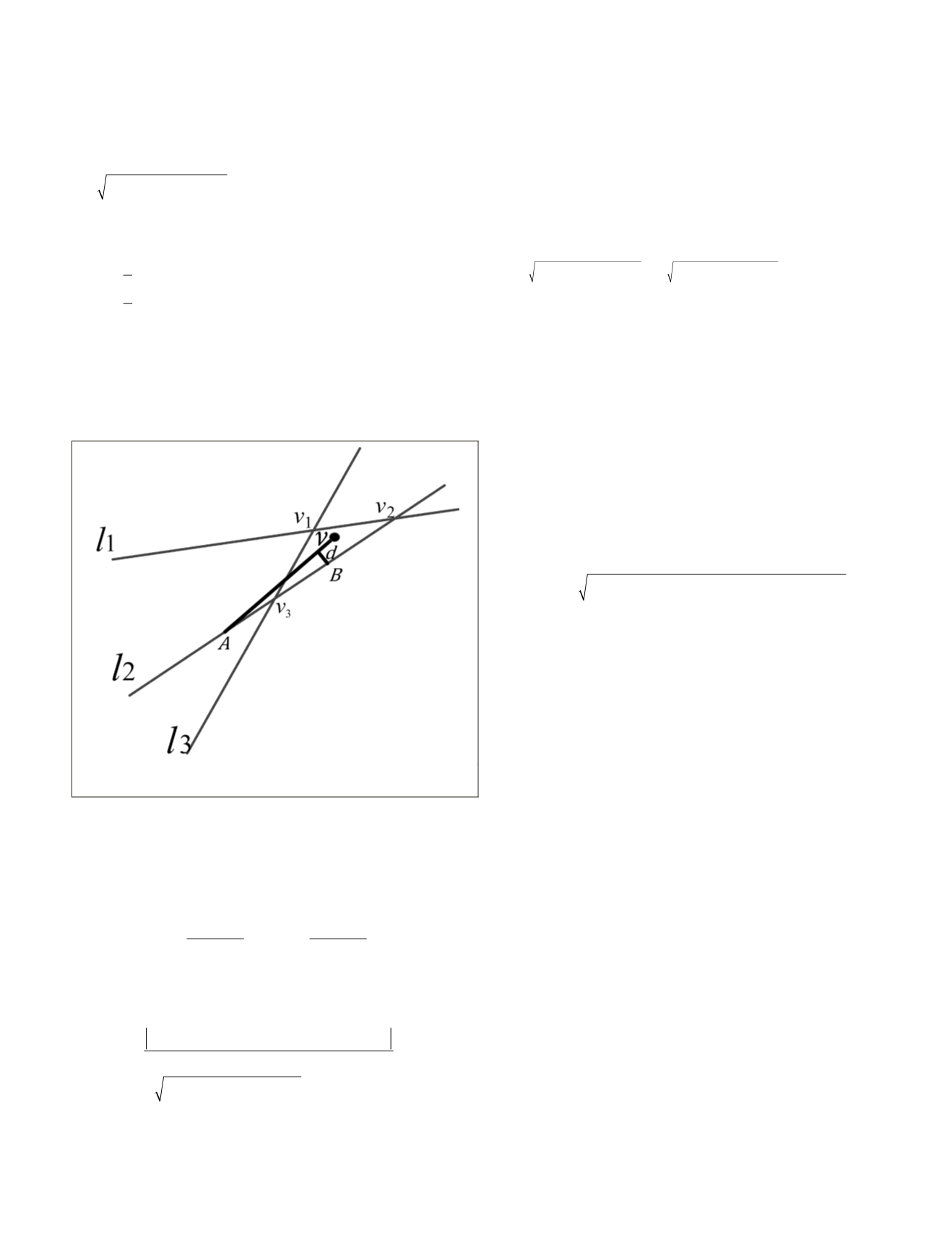
Figure 2. Relationship between straight lines and vanishing point
under the influence of radial distortion.
In Figure 2,
l
1
,
l
2
,
l
3
represent the projection of parallel
lines in the image space and their intersections are
v
1
,
v
2
,
v
3
, respectively. The actual vanishing point
v
(
x
v
,
y
v
).
A
(
x
A
,
y
A
)
and
B
(
x
B
,
y
B
) is assumed at the point. are respectively any two
points on the line segment
l
2
. The straight line through point
A
and
v
can be expressed as
y
y y
x x
x y
y y
x x
x
v A
v A
A
v A
v A
A
= −
− + − −
−
.
Thus, the distance
d
from the point
B
to the line segment
l
Av
is
established.
d
x x y y y y x x
s
s
x x y y
B A v
A
B A v
A
Av
Av
v
A
v
A
=
−
(
)
−
(
)
− −
(
)
−
(
)
≡
= −
(
)
+ −
(
)
0
2
2
(4)
here,
S
Av
represents the length of the line segment
Av
. In the
ideal situation of no distortion, the three points
A
,
B
,
v
should
be on a straight line making that the distance
d
should be 0
(Grammatikopoulos
et al
., 2007; González-Aguilera
et al
.,
2011). Let
A
(
x
A
,
y
A
),
B
(
x
B
,
y
B
) be the distorted points in the im-
age, and
r
A
,
r
B
be the distortion radius of the distorted points
A, B
, respectively. Then, for
j
= 1,2 …
m
straight lines with
i
= 1,2 …
n
pairs of points in each straight line, the following
expression is established by the Equations 3 and 4.
F x k r x x x k r x x y y k r
ij
B
B B
A A A
v
A A
= +
− − +
−
− +
(
)
(
)
(
)
(
)
1
1
1
2
0
2
0
2
y y
y k r y y y k r y y
A
B
B B
A A A
−
− +
− − +
−
(
)
(
)
(
)
(
)
(
0
2
0
2
0
1
1
)
(
)
(
)
(
)
(
) (
)
− +
−
= − + −
2
2
x x r x x
r
x x y y r
v
A A A
A
A
A
2
0
0
0
,
B
B
B
x x y y
= − + −
(
) (
)
0
0
2
2
(5)
Equation 5 is the observational equation for the adjustment
of all line segments. The unknown parameters are vanish-
ing points (
x
v
,
y
v
) and the first radial distortion coefficient
k
1
,
which can be optimized by using a least squares adjustment.
The Interior Orientation Parameters Calculation
It is well known that camera calibration from a single image
can be performed based on three vanishing points associated
with three mutually orthogonal straight lines in the object
space. According to the properties of vanishing points, the
principal point is the orthocenter of the triangle with vertexes
in the three vanishing points associated with three mutu-
ally orthogonal straight lines in the object space (Caprile and
Torre, 1990). Hence, the principal distance can be calculated
from any two vanishing points
v
1
(
x
v
1
,
y
v
1
) and
v
2
(
x
v
2
,
y
v
2
) corre-
sponding to perpendicular lines in the object space:
c
x x x x y y y y
v
v
v
v
=
−
− + −
−
(
)
- (
)(
) (
) (
)
1
2
1
2
0
0
0
0
.
(6)
Since vanishing points are sensitive to noise and the dis-
tortion center is not simply at the image center, the results of
camera calibration have relatively low accuracies. In this pa-
per, the principal point and principal distance are optimized
by utilizing line segments and an ellipse in the image.
Orthogonal Vanishing Points Pairs
The pole-polar relationship: A point
x
and conic
C
define a
line
l
=
Cx
. The line
l
is called the polar of
x
with respect to
C
, and the point
x
is the pole of
l
with respect to
C
. The point
x
and line
l
are pole-polar with respect to conic
C
. If the point
y
is on the line
l
=
Cx
, then
y
T
Cx
= 0. Any two points
x
,
y
sat-
isfying
y
T
l
=
y
T
Cx
= 0 are conjugate with respect to
C
(Hartley
and Zisserman, 2000). (Figure 3a)
Orthogonal Vanishing Point Pairs
Suppose two points
v
1
,
v
2
are the vanishing points of two dif-
ferent directions in the object plane; if the two directions are
orthogonal, then the two points
v
1
,
v
2
are conjugate with re-
spect the conic
C
, satisfying
v
T
2
Cv
1
= 0. The two points
v
1
and
v
2
are called as an orthogonal vanishing point pair (Hartley
and Zisserman, 2000). (Figure 3b)
As shown in Figure 3b, the vanishing point
v
1
and line
l
are pole-polar with respect to the conic
C
, i.e.,
l
=
Cv
1
. Sup-
pose the vanishing point
v
2
, which is the intersection of the
polar line
l
and the vanishing line
l
∞
, then
v
1
and
v
2
are a pair
of orthogonal and conjugate vanishing points, i.e.,
v
T
2
l
=
v
T
2
Cv
1
= 0. Thus, given any vanishing point
v
1
, its orthogonal vanish-
ing point
v
2
can be calculated by
l
∞
=
v
1
×
v
2
,
l
=
Cv
1
,
v
2
=
l
×
l
∞
(7)
Therefore, given an ellipse and a vanishing line which lies
on the plane defined by the ellipse, multiple pairs of orthogo-
nal vanishing points can be obtained by the Equation 7.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
May 2016
327


