• Second Criterion - The Chance to Have Correspon-
dence in Object Space:
A similar procedure to the
above second factor (Figure 3) is applied, but here
based on all three true-lengths of the line-segments
forming a triangle. This criterion is used to specify the
importance of the triangles based on the fact that pat-
terns with longer true-lengths are more likely to have
correspondence in object space. Hence, higher weights
(e.g.
Quality
–
Element
j
3
) are assigned to them.
• Third Criterion - The Number of Crossing-Lines:
The fi-
nal weighting factor is the number of crossing-lines for
each pattern. This factor can influence the output of the
HQPS
-phase as well as the success of the
SLIM
process
by selecting proper triangles. Here, a weight (e.g.,
Qual-
ity
–
Element
j
4
) is devoted to each triangle based on the
normalized number of its crossing-lines.
Finally, the total-score of each triangle (
j
= 1 to number of pos-
sible patterns in image space) is computed through Equation 2:
Total Score
p Quality Element
p
j
i
i
j
i
i
−
=
−
=
=
∑
∑
1
4
1
4
( *
)
i
(2)
Here, the coefficients of
p
i
are the impact-factors of the
above mentioned four quality-elements and specify the
importance of them. In the next section, different values of
impact-factors are tested practically.
The computed total-score (i.e., assigned to all the remain-
ing patterns) are used to exclude the weak triangles in favor
of time efficiency of the next matching-phase. For this reason,
only
R
triangles with highest total-score values are selected to
test their correspondence in matching-phase where
R
is deter-
mined using the following experimental relation (Equation 3).
R ln l
l k k
=
−
(
)
!
! !
(3)
Here,
k
is three (the number of line-segments in each tri-
angle), and
l
is the number of fine-quality-lines in image space
(i.e., line-segments larger than mean length).
Phase 2: The Procedure of Automatic Matching
This phase is iteratively implemented for all the
R
optimal
triangles (found in the previous
HQPS
-phase) when a proper
triangle is looked for in the object space. Therefore, different
steps of the proposed matching-phase are performed for
i
th
im-
age space triangle {
i
= 1:
R
} following the procedure.
1. All the possible triangles in the object space (i.e.,
three-combinations of
N
line-segments when the order
is important) are generated for each
R
triangles
.
The
combination of the image space triangle (
i
) and these
produced object space triangles are regarded as match-
triangles-candidates.
2. Then, instead of investigating the correspondence of all
match-triangles-candidates, a screening-procedure is
applied to exclude the improper ones. This exclusion
is effective in computational time. This procedure aims
to remove the improper match-triangles-candidates
based on some invariants between the image-triangle (
i
)
and object-triangles. For this reason, four invariants are
selected including inner relative angles, ratio of generat-
ed-lengths as well as transformation correctness and
accuracy. These criteria are introduced in the following.
• Inner Relative Angles Criterion
: Although conjugate
lines in the image and object spaces are differently
oriented, it is expected that their inner relative angles
to be rather the same by a small threshold. This thresh-
old (called
T
1
) is due to noise and quantization and
depends on geometrical characteristics of the datasets.
Based on our experiments, (0, 5] degrees is a proper
range for
T
1
. Higher values increase the initial search
space and impose additional computational efforts.
• Ratio of Generated-Lengths Criterion
: Similar to the
first criterion, conjugate lines have different generated-
lengths in different spaces (i.e., image and object
spaces). However, it is expected that the length ratios to
be rather the same between image and object spaces by
a small threshold (i.e.,
T
2
). Based on our experiments
on high resolution images (0, 0.5] is a proper range for
T
2
. Again, higher values only increase the search space
and also the computational time.
• Correctness Evaluation of a Transformation
: As men-
tioned earlier, an
MGL
is generated by the extension and
intersection of true line-segments. Two triangles are
matched, if their true-lines as well as their
MGP
s and
MGL
s
are also matched together. Using the
MGP
s of a pair of two
triangles (the match-triangles-candidates), the parameters
of a 2D affine transformation can be estimated. This crite-
rion is based on this transformation where the end-points
of the true-lines are transformed to image space through
the solved transformation. A pair of true-lines is assumed
to be matched if one of the following conditions in Figure
4 is satisfied after applying the transformation.
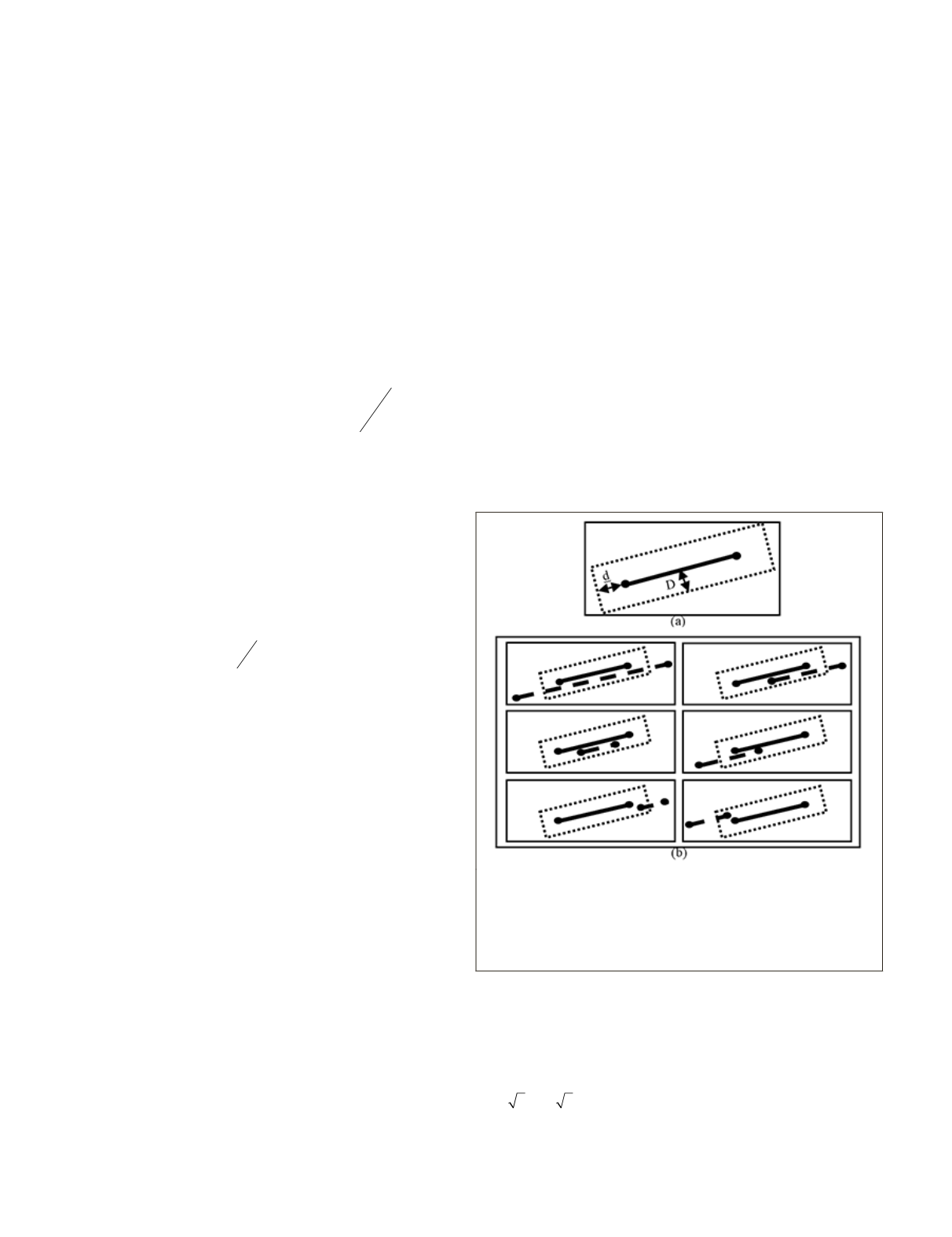
Figure 4. (a) the round dot rectangle are the boundary of accep-
tance (
D
&
d
< =
T
3
) which are defined in image space, and (b)
the dash lines as well as continuous lines are transformed lines
from object space to image space and their conjugate lines in
image space, respectively. Additionally, the black circles are their
transformed as well as true end-points.
The boundary of acceptance in Figure 4a is defined ac-
cording to the existence of some errors such as computa-
tional errors as well as the applied extraction methods and
fragmentation. In Figure 4a,
D
is the maximum acceptable
distance (such as Euclidean or Hausdorff distance) between
a transformed line and its candidate match. Additionally,
defines the maximum acceptable tolerance of end-points
d d d
x
y
=
=
(
)
2
2 .
The thresholds of
D
as well as
d
x
and
d
y
prevent select-
ing collinear line-segments which are not in the acceptance
368
May 2016
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


