PE&RS May 2016 - page 366

present automatic registration methods based on collinearity or
coplanarity equations for aerial images (Habib and Kelley, 2001;
Junior and Tommaselli, 2013; Akav et al., 2004; Jaw and Perny,
2008). A detailed review in the field of using linear features and
collinearity condition and its advantages in comparison to co-
planarity condition can be found in the works of Schenk (2003)
and Schenk (2004). In addition to parametric models, some re-
searchers attempt to use non-parametric models in registration
purposes (Liu et al. 2012; Song et al., 2013). For example, an
automatic vector map to HRSIs registration is performed using
rational polynomial coefficients (RPCs) as the initial orientation
parameters (Lu et al., 2013). In the work of Zang et al. (2011) for
UAV remote sensing imageries registration, straight linear fea-
tures and a Modified Iterated Hough transform (MIHT) are used
to estimate the parameters of an affine transformation.
Most of the previous matching methods need some a priori
information such as interior orientation parameters (IOP),
exterior orientation parameters (EOP ), and RPCs or three initial
corresponding features for the matching step. Hence, these
methods are not a general model to be used for all types of
sensors. Additionally, sensor information is not always avail-
able. On the other hand, non-parametric models can be used
successfully due to their unique characteristics such as gener-
ality. These models do not need any initial information about
the image geometry. The main disadvantage of these methods
is their need for many well-distributed ground control points
(GCPs). However, because of the improvements on accuracy as
well as reducing the need for GCP s using meta-heuristic meth-
ods (Valadan Zoej et al., 2007; Yavari et al., 2013), they have
the high potential to be used in automatic registration.
In this paper, a novel structural linear feature-based match-
ing method (SLIM) designed based on non-parametric models is
proposed for high resolution image to map matching purposes.
The paper is organized as follows. In the next Section , the
novel SLIM procedure is introduced including its concepts,
high-quality pattern selection procedures and finally, its auto-
matic structural matching in detail. The experimental results
and accuracy assessments are presented and discussed ending
with Conclusions.
Automatic Image to Map Matching Methodology Based on SLIM
Procedure
As the input of the proposed SLIM, it is assumed that some
line-segments are previously extracted from both image and
map spaces. As an important point, these line-segments
should not be necessarily identical in their end-points. This
highly facilitates their independent extraction from both the
image and the map.
The goal of the proposed SLIM is to automatically and in a
time efficient manner determine the correspondence between
these lines by finding two specific corresponding patterns. In
this research, the specific patterns are selected among all pos-
sible three-combinations of lines forming a triangle.
This novel method is done in three main phases described
as follows:
• First phase: Optimum high-quality-patterns of image
space are selected through a new weighting strategy
called high quality pattern selection or HQPS-phase.
These selected patterns are iteratively introduced to the
second phase as the input-triangles.
• Second phase: For each input-triangle, all the possible
pairs in object space are generated. Improper ones are then
excluded using four geometric constraints. For the remain-
ing ones, the correspondence of the other crossing lines
are also determined simultaneously using the proposed
constraints. In each iteration, a pair with maximum num-
bers of conjugate-lines is considered as the local “winner.”
In this paper, this phase is called the matching-phase.
• Third phase: In the final-phase, among all the local win-
ners of the second phase, a pair with maximum numbers
of conjugate-lines is selected globally. These lines are con-
sidered as the initial matched-lines to find the correspon-
dence of all other lines using the proposed constraints.
In the first subsection, the new concepts are explained. The
three phases of the SLIM are discussed in detail in the follow-
ing subsections.
The Concepts Applied in the SLIM Procedure
As mentioned earlier, the extracted lines in image and object
spaces do not have necessarily conjugate end-points. In
addition, a line may be fragmented to some segments or its
position may be changed due to noise, occlusion, or ap-
plied extraction methods. To deal with these problems, new
concepts compatible with the existing mathematical methods
in photogrammetry and remote sensing are applied which are
introduced in the following.
Through these new concepts, the lines which are math-
ematically generated by extension and intersection of
line-segments are applied. These lines are called math-
ematically generated lines (MGL s for brief). These MGL s
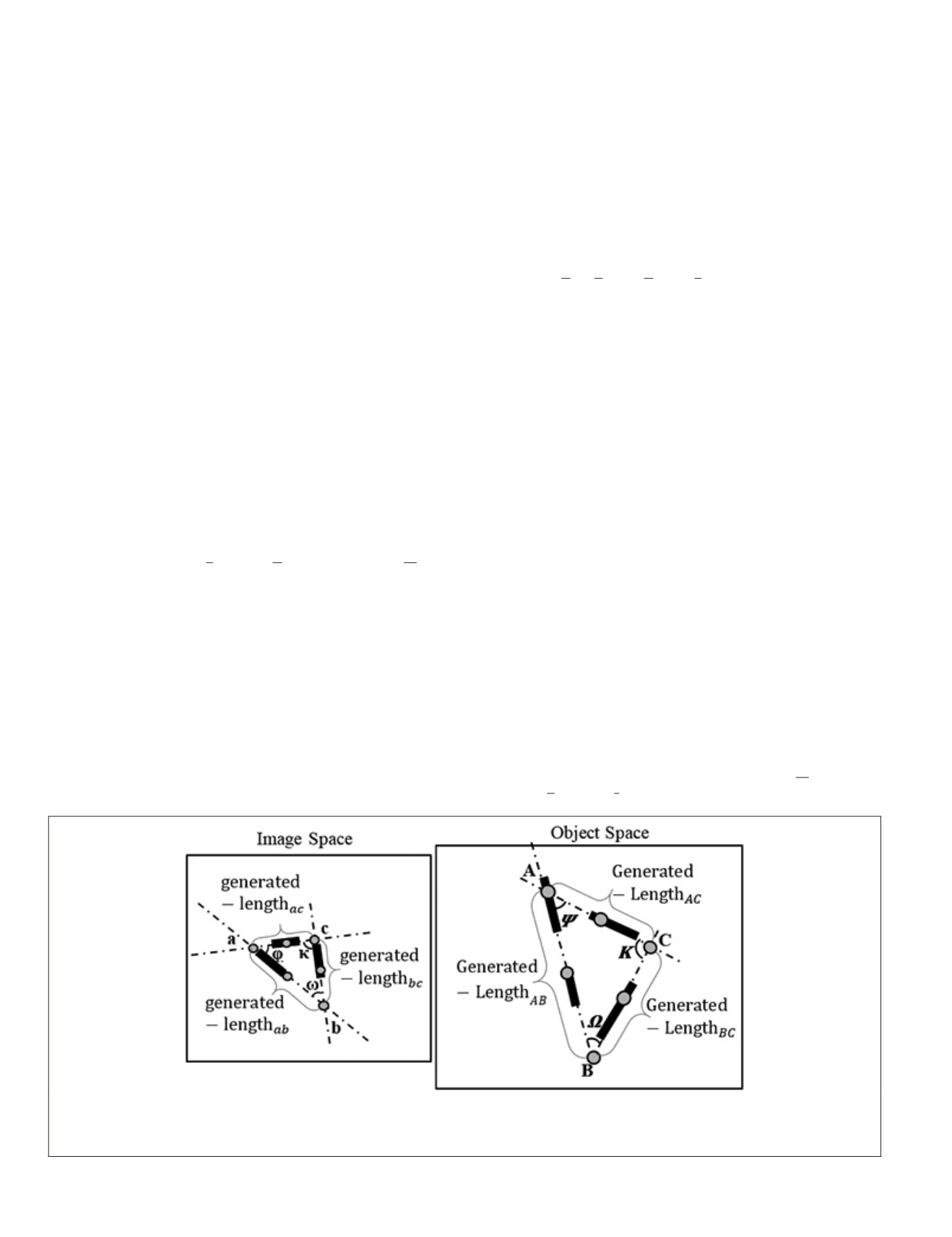
are used to form the sides of the triangles (Figure 1). Each
Figure 1. Extracted conjugate line-segments are shown in thick black continuous form in image and object spaces. The dash lines are the
extension of line-segments which produce MGL s. By intersection of MGLs, a pattern (e.g., triangle) is formed. The grey circles are consid-
ered as MGP s (the vertexes or the mid-points of MGLs). The characteristics of the generated-pattern such as three inner relative angles
(ω, φ, κ) and (Ω, Ψ, Κ) in image and object spaces as well as generated-lengths are also shown.
366 May 2016 PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING