J
h
h
=
B A
0
0
(59)
and the
χ
2
1
-distributed test statistic reads:
T
d
⊥
⊥
⊥
=
2
2
σ
(60)
For further conceivable constraints and the corresponding
tests please refer to Heuel (2004) and Förstner and Wrobel
(2016, p. 304ff).
Selecting Consistent Constraints
Once all potential relations are tested, we have a set of con-
straints at hand. These result from those hypotheses which
could not be rejected by the tests. For the final adjustment, a
set of consistent, i.e., non-contradicting, and non-redundant
constraints is mandatory since redundant constraints will
lead to singular covariance matrices. Since we are dealing
with imprecise and noisy observations, we have to face the
possibility of non-rejected hypotheses which are contradic-
tory. We utilize the greedy algorithm proposed in Meidow and
Hammer (2016) and Meidow
et al
. (2009) to automatically
select a set of consistent constraints.
Experiments
The proposed approach provides covariance matrices for
plane parameters corresponding to given polygons. First of
all, we compare covariance matrices obtained in this way
with estimated covariance matrices for plane parameters
based on points sampling the polygons’ areas. The approach
is then used for the task of building reconstruction by geomet-
ric reasoning.
Model Validation
We are able to compute covariance matrices for a polygon
represented either by its vertices or by a corresponding point
cloud sampling the polygon’s area. For the former case we
have to specify an assumed virtual sampling distance
Δ
. In
both cases we have to specify an uncertainty
σ
of the point
coordinates in direction of the polygon’s normal. In the fol-
lowing, we denote the analytically derived covariance matrix
with
Σ
0
and the estimated covariance matrix by
Σ
ˆ
.
Since we are utilizing homogeneous coordinates, the 4×4
covariance matrices (Equation 23) of the plane parameters are
singular. For the comparability of the theoretical and empiri-
cal covariance matrices
Σ
, we reduce them with the Jacobian:
J
=
r r
1 2
0
0 0 1
(61)
of the 4-vector
A
representing the plane, i.e.,
Σ
:=
J
Σ
J
to
eliminate the zero-uncertainty in the length of the normal
vector and to obtain regular 3×3 matrices.
The distance of the two covariance matrices can then be
conveniently be described by the
U
positive eigenvalues
λ
u
of
the matrix
Σ
ˆ
·
Σ
+
0
which can be interpreted as the ratios of the
variance in
Σ
ˆ
and
Σ
0
.
The average squared logarithm of the ratios
(
)
(
)
d
U
u
U
u
2
0
1
2
0
1
ˆ
ˆ
,
Σ Σ
λ
Σ Σ
=
=
+
∑
ln
.
(62)
is invariant w.r.t. a swap of the two matrices and describes
the average deviation of the ratios from one (Förstner and
Moonen, 1999, p. 121). The transition to the consideration
of the standard deviations provided by the matrices, is then
achieved by computing:
d
d
′
,
/
Σ Σ
0
2
(
)
=
(
)
exp
(63)
the average deviation of the ratios of the standard deviations
from one. A value of
d
′
= 1.1 indicates the standard deviations
to differ by 10% on average.
For validation, we executed a simulation with 10,000 trials
each. In each trail a non-degenerated triangle with uniformly
distributed vertex coordinates in the range [−1, 1] has been
created in 3D space. In the corresponding plane, the poly-
gon’s area has then been sampled with 3D points on a regular
grid with spacing
Δ
= 0.05. Normally distributed noise with
σ
= 0.02 has then been added to the point coordinates in the
normal’s direction.
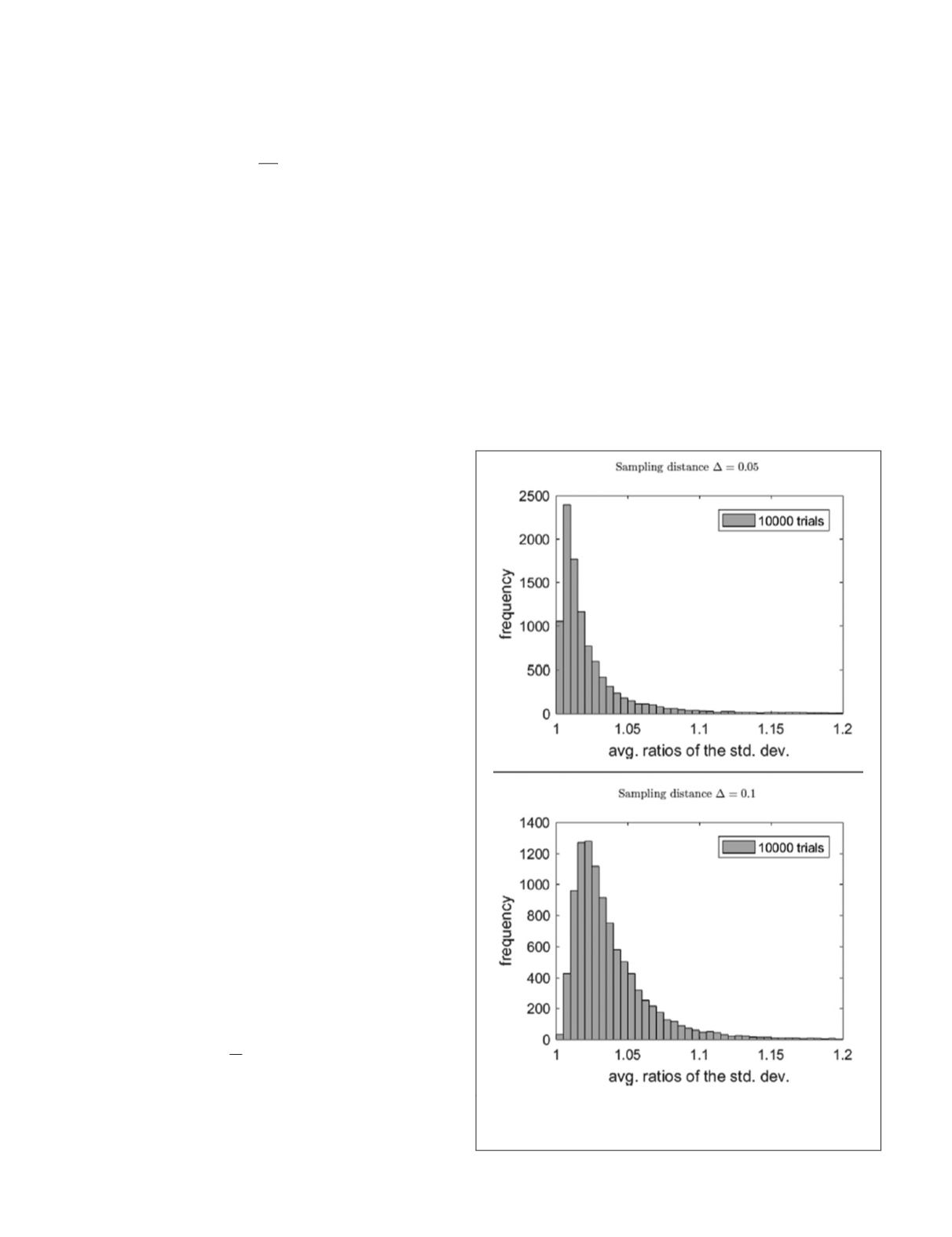
Figure 2 shows the histograms for the distance measure
(Equation 63) obtained for sampling distances
Δ
= 0.05 and
Δ
=
0.1. The results are better for smaller samplings distances, but
independent on the choice of the standard deviation
σ
. Ninty
percent of the ratios differ by less than a factor of 1.05 and
1.07, respectively. This demonstrates that the integral expres-
sions for the covariance matrices are valuable approximations.
Figure 2. Histograms of the distance measures (63) obtained
by 10,000 simulation runs for the sampling distances
Δ
=
0.05 (top) and
Δ
= 0.1 (bottom).
398
June 2018
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


