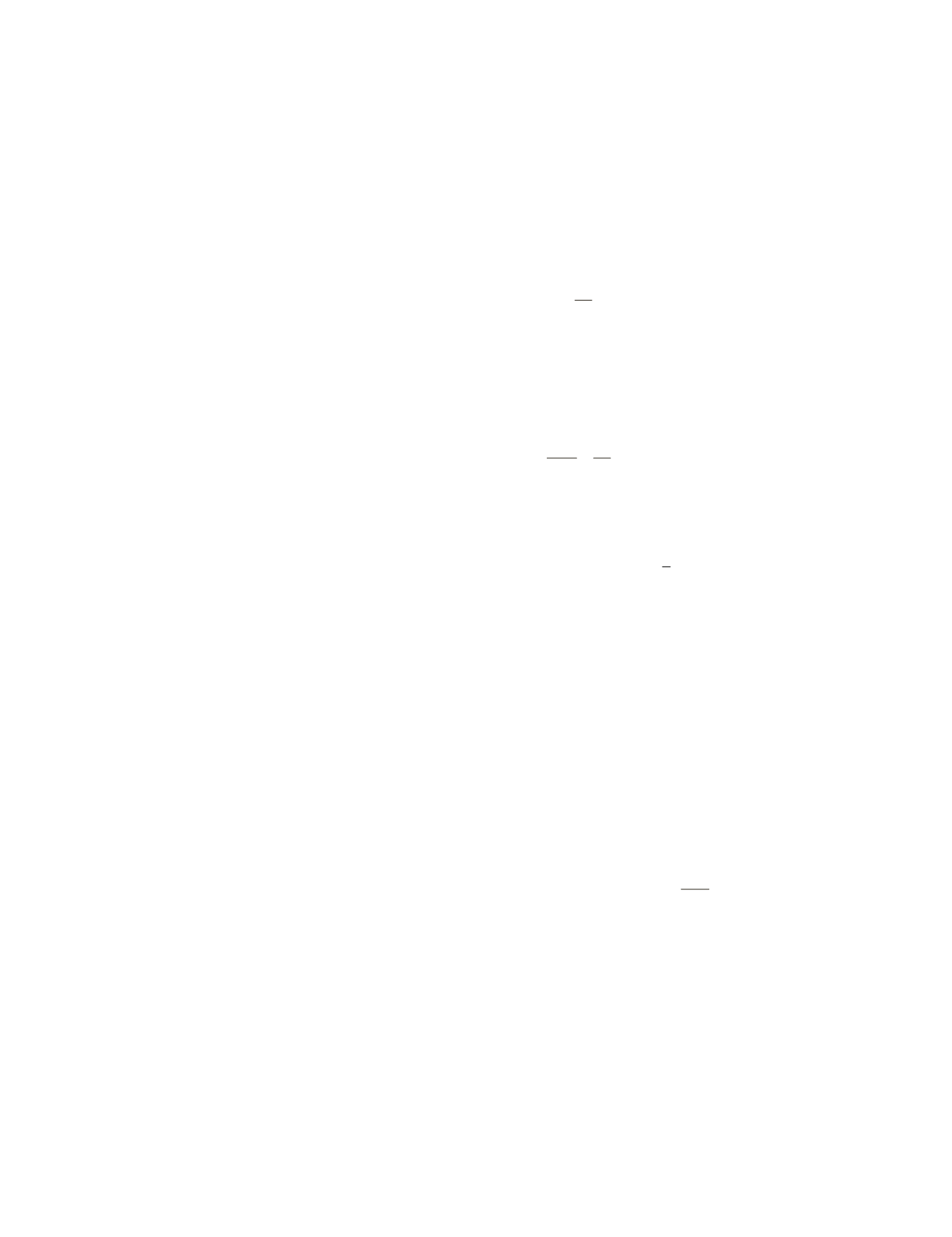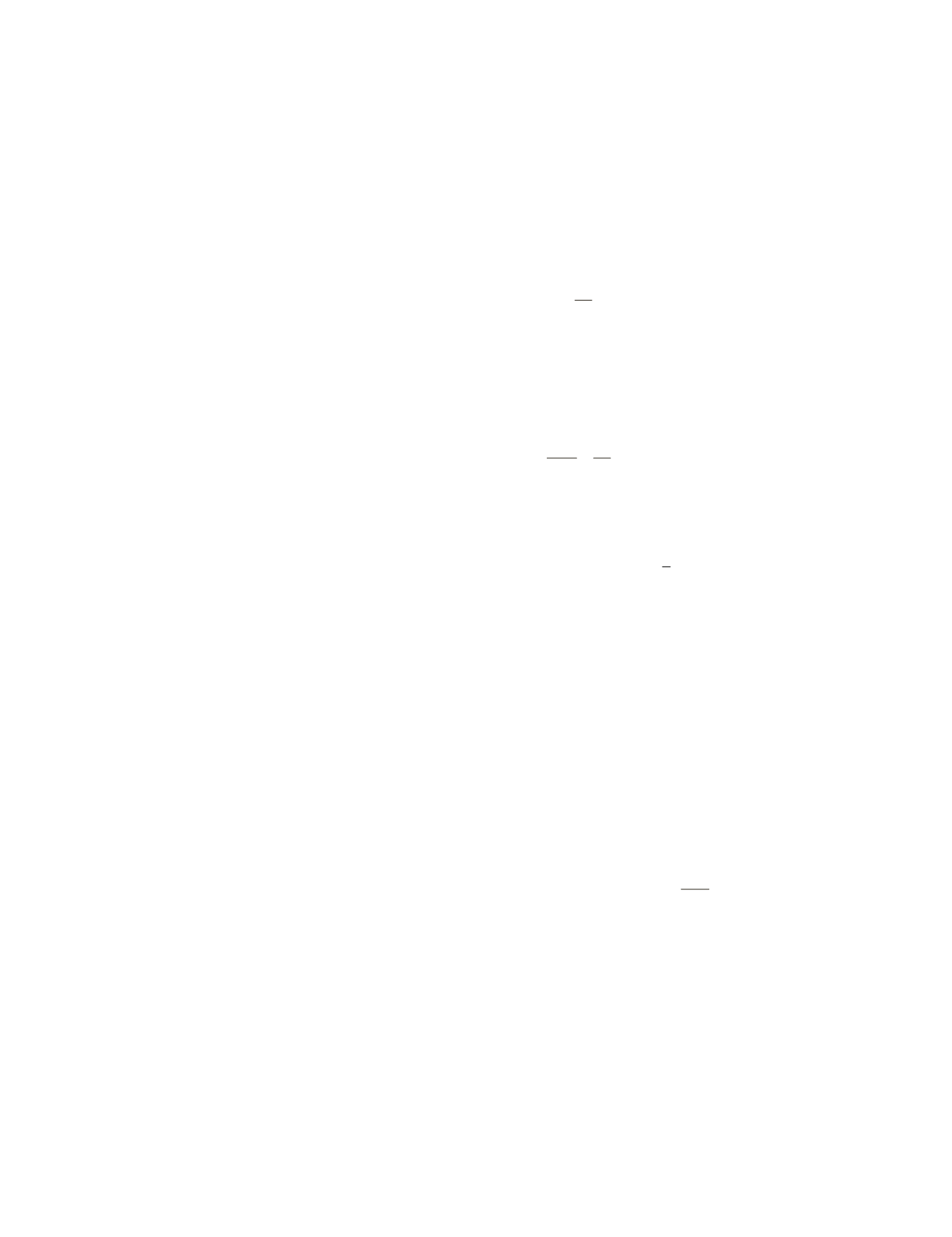
replaced by integrals. This idea implies the assumption that
the points are distributed uniformly on the planar patch. We
extend this approach to multiply-connected regions and to
planar polygons embedded in 3D space. Methodologically,
this is a refinement of the determination of the covariance
matrix for the centroid representation given a point cloud
representing a planar patch (Förstner and Wrobel, 2016, p.
397 and p. 436).
This paper is a revised and extended version last year’s
publication (Meidow and Förstner, 2017). The presentation
is enriched by a more detailed explanation of the reasoning
process and a model validation step. The latter is achieved
by the experimental comparison of theoretical and empirical
covariance matrices.
To demonstrate the feasibility and the usefulness of the ap-
proach, we describe a complete stochastic reasoning process
for a building that comprises the determination of the planes’
uncertainties, the inference of geometric relations, and even-
tually the enforcement of the deduced constraints by adjust-
ment.
Theoretical Background
After clarifying our notation, we present in the following
sections the centroid representation of planes, the estimation
of the corresponding parameter values, and the estimation of
the accompanying covariance matrix. For the determination
of the normal equation matrix, sums of coordinate moments
have to be computed. These sums are then replaced by inte-
grals to perform the transition to analytical expressions for
the covariance matrix of plane parameters given a 3D planar
polygon.
Notation
We denote geometric 2D entities, namely points, with lower-
case letters and 3D entities, namely 3D points and planes,
with upper-case letters. For the representation of points,
planes and transformations, we utilize also homogeneous
coordinates. Homogeneous vectors and matrices are denoted
with upright letters, e.g.,
x
or H, Euclidean vectors and
matrices with slanted letters, e.g.,
x
or
R
. For homogeneous
coordinates ‘=’ means an assignment or an equivalence up
to a scaling factor
λ
≠
0. We distinguish between the name of a
geometric entity denoted by a calligraphic letter, e.g.,
x
, and
its representation, e.g.,
x
or
x
. We use the skew-symmetric
matrix
S
(
x
) to induce the cross product
S
(
x
)
y
=
x
×
y
of two
vectors. The operation
d
= diag(
D
) provides the diagonal ele-
ments of the matrix
D
as vector
d
.
D
= Diag(
d
) constructs the
diagonal matrix
D
based on the vector
d
and
D
= Diag(
A,B,…
)
constructs the block-diagonal matrix
D
based on the given
matrices {
A,B,…
}.
Plane Parameters and their Uncertainties Given a 3D Point Cloud
For the representation of an uncertain plane we utilize the
centroid form, as it naturally results from the best fitting
plane through a set of given points. The presentation com-
prises the centroid
X
0
where the uncertainty of a point on the
plane is smallest, the rotation matrix
R
for the transformation
of the plane into a local coordinate system, the maximum and
minimum variances
σ
2
α
and
σ
2
β
of the plane’s normal, and the
variance
σ
2
q
of the position of
X
0
across the plane. Thus the
nine parameters compiled in
{
X
0
,
R
;
σ
2
q
,
σ
2
α
,
σ
2
β
},
σ
2
α
≥
σ
2
β
(1)
constitute a convenient representation (Förstner and Wrobel,
2016, p. 436).
For the estimation of the plane parameters we consider the
distances of the given
I
points
X
i
,
i
= 1 …
I
to the best fitting
plane
A
. Given a point
X
0
on
A
, the point-plane distances
read
d
(
i
,
A
) =
N
(
X
i
–
X
0
)
(2)
with the plane’s normal
N
and the points in Euclidean rep-
resentation. With the squared distances of the least-squares
method the objective function is:
L
wd
i
i
I
=
=
∑
2
1
( , )
X A
(3)
=
−
−
=
∑
1
2
1
0
0
σ
N X X X X N
i
I
i
i
(
)(
)
(4)
We assume independent and identically distributed point
coordinates with the weight
w
= 1/
σ
2
for all observations. For
the estimation of plane parameters with individual weights
for the points, please refer to (Förstner and Wrobel, 2016, p.
436). Setting the derivative to zero,
∂
∂
=
− +
=
=
∑
L
i
i
I
X
N
X X N
0
2
0
1
1
2 2
0
σ
(
)
(5)
reveals that the relation is fulfilled for the centroid
X
0
with
the coordinates
X
X
0
1
1
=
=
∑
I
i
i
I
(6)
For the determination of the plane’s orientation we com-
pute the eigendecomposition of the matrix of second central-
ized moments
M
i
i
i
I
=
−
(
)
−
(
)
=
∑
X X X X
0
0
1
(7)
=
=
=
∑
R R
k k k
k
Λ
λ
r r
1
3
(8)
with the three eigenvalues
λ
1
≥
λ
2
≥
λ
3
in
Λ
= Diag([
λ
1
,
λ
2
,
λ
3
])
and the orthonormal matrix
R
= [
r
1
,
r
2
,
r
3
]. The normal of the
plane is then
N
=
r
3
.
The third eigenvalue is the sum of the squared residuals,
thus the estimated variance of the point coordinates can be
derived from:
ˆ
σ λ
2
3
3
=
−
I
(9)
assuming no outliers are present. If the redundancy
I
–
3
is
large enough, the estimated variance
σ
ˆ
2
can be used to fix the
weight
w
.
In the following, we assume the original point cloud data
not to be available, and only the shape of the planar patches
is known; hence we need to make assumptions on
σ
2
and the
distribution of the 3D points.
For the specification of the plane’s uncertainty in form of
a covariance matrix we centralize and rotate the given points
in a way that the best-fitting plane for the resulting points is
A
′
= [0,0,1,0]
, i.e., the XY-plane, and the X- and the Y-axis
correspond to the two major axes
r
1
and
r
2
of the moment ma-
trix (Equation 7). The transformation is achieved by using the
centroid
X
0
and the rotation matrix
X
R
. The covariance matrix
is invariant w.r.t. this motion.
394
June 2018
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING