PE&RS July 2015 - page 548

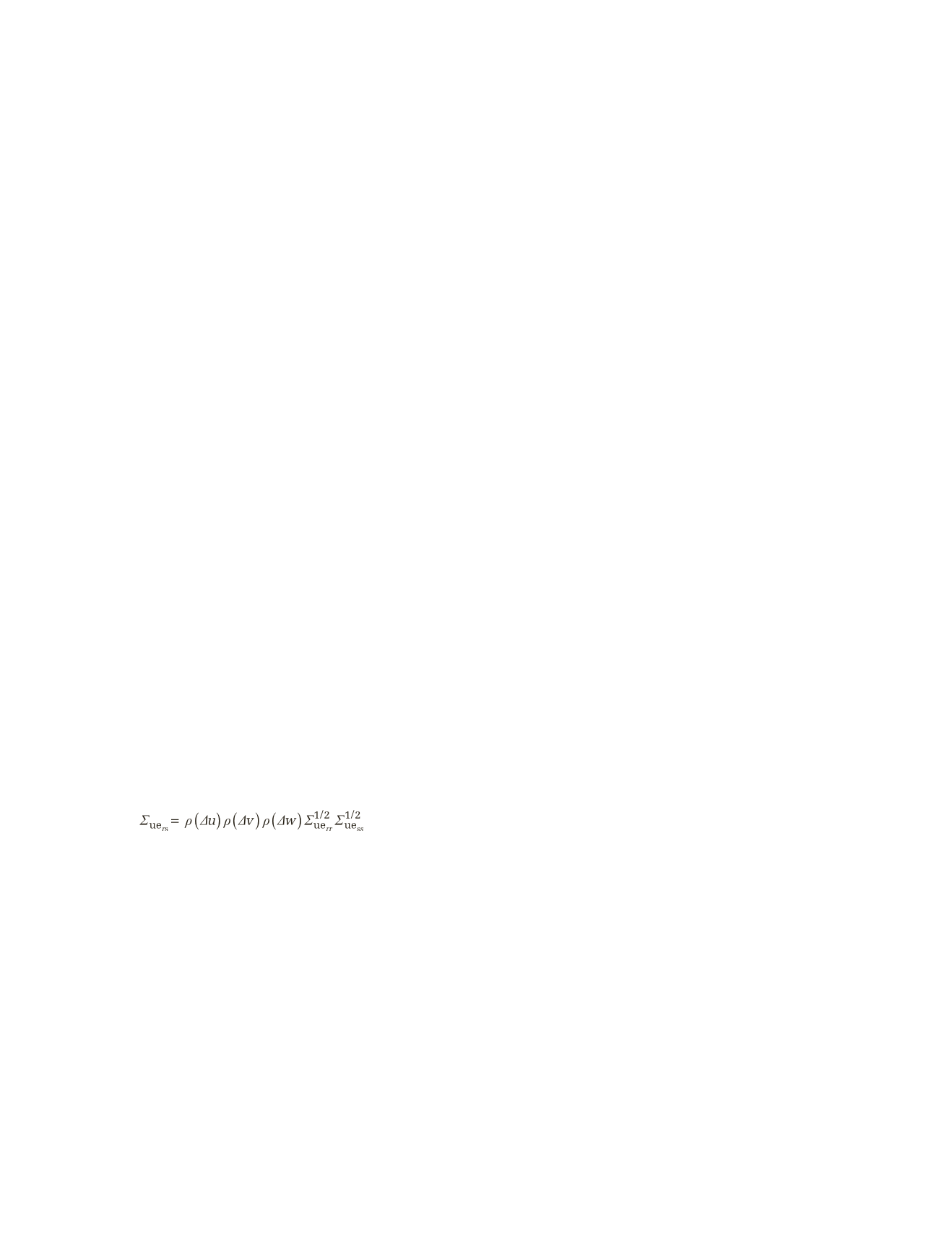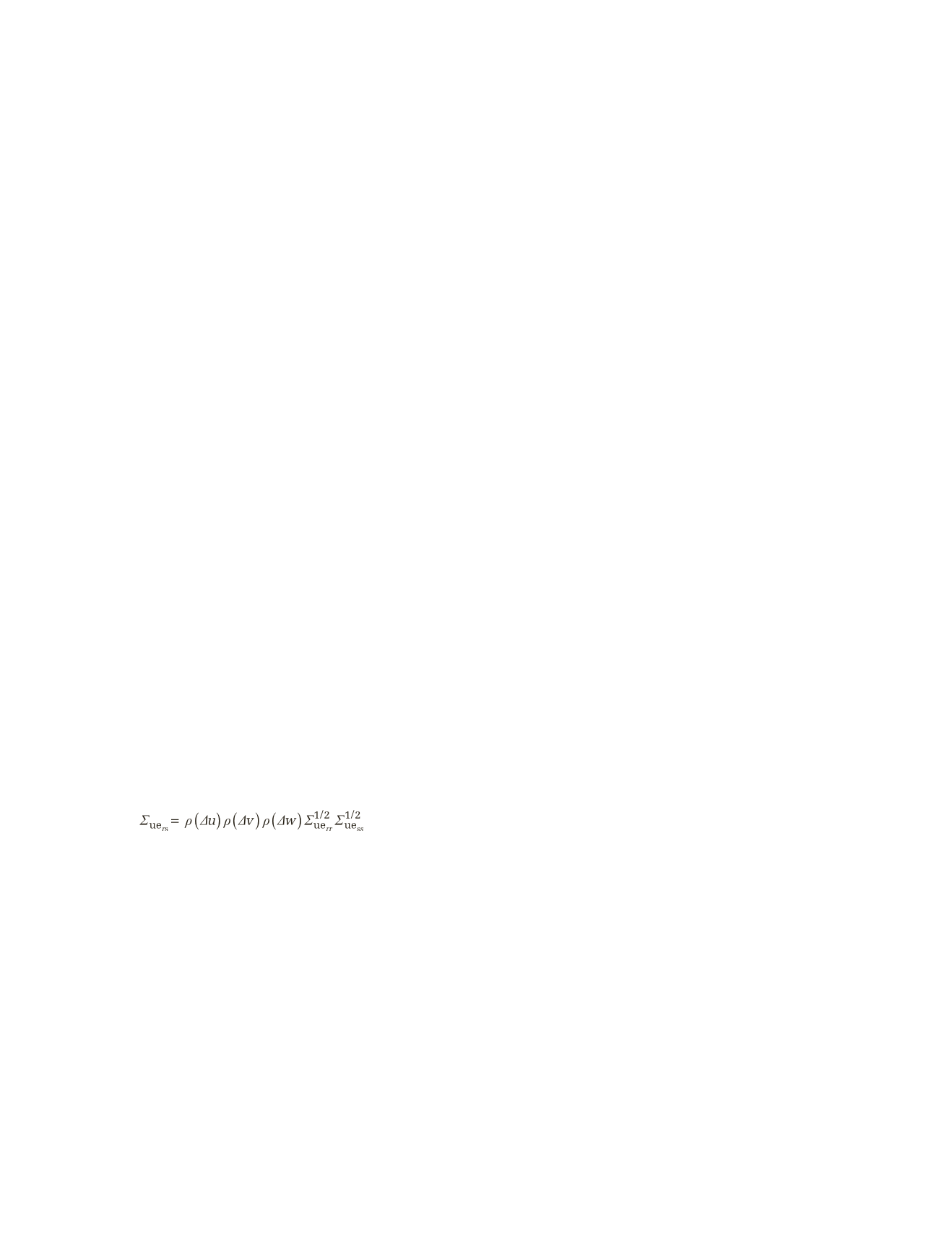
• Sensor position uncertainties (σ Δx, σ Δy, σΔ z),
• LOS angle uncertainties (σθ1, σθ2, σθ3), and
• Range measurement uncertainty σ Δr.
An additional uncertainty is related to the physical features
of the terrain. For linear-mode lidar, each pulse of the lidar
sensor illuminates the terrain with a finite-size beam which
intersects features with potentially different reflectance proper-
ties and different heights. This leads to significant variations
in the return pulse shape and magnitude, adding error to the
range calculation (Schaer et al., 2007). Capturing an estimate
of the aggregate range uncertainty for each point in the point
cloud is a valuable piece of metadata to have available for ULEM
if possible. If available and pre-calculated, this error could be
captured as a per-point uncertainty and included as a random
contributor to the mensuration error during exploitation. Since
the total variation across the dataset for these values is ex-
pected to be small and the precision does not have to be fine,
implementing a pointer per point-record that references a look-
up table of representative per-point uncertainty values (the six
elements that comprise the upper triangular portion of a 3 × 3
covariance matrix) would provide an efficient storage mecha-
nism. If instead this per-point uncertainty is computed by
exploitation software at time of mensuration, it can be captured
as a processing-error contribution to mensuration error.
The error contributors not captured in the top-level ULEM
sensor parameters are represented using unmodeled error
(Doucette et al., 2013). Unmodeled errors (UE) cannot be practi-
cally characterized by the physical sensor model’s support-
data adjustable parameters, hence they cannot be corrected or
removed through a registration or triangulation process. An ex-
ample of this in traditional photogrammetry is lens distortions
for which the model may not provide associated parameters for
adjustment. Unmodeled error provides a placeholder for high-
frequency error to supplement the adjustable parameter error,
and is represented by both covariance and cross-covariance
terms. UE is not totally random; therefore its cross-correlations
between points are non-zero (for small distances or small tem-
poral changes) and are typically modeled by an SPDCF based on
spatial distance. Since the axes for UE correlation may not align
with the LCS axes, a ( u,v,w) system is defined (e.g., u defined
along a collection strip, v defined across the strip, w complet-
ing a right-handed system). Correlation coefficients (ρ) are
computed based on the spatial distance between points in each
dimension (Δu, Δv, Δw). The unmodeled error cross-covari-
ance between two points (r and s) is then computed by:
(6)
where Σuers represents the cross covariance, (ρ(Δu), ρ(Δv),
ρ(Δw)) represent the correlation coefficients in the u, v, and
w directions respectively, Σuerr represents the UE covariance
at point r, and Σuess represents the UE covariance at point s
(the superscript ½ indicates the principal matrix square root
which is computed by Singular Value Decomposition (SVD))
In most cases, UE is determined by empirical means, such
as performing data adjustments in areas with much control
data, providing initial estimates of the UE and its correlations,
and refining these estimates until the resulting reference vari-
ance approaches unity (Doucette et al., 2013).
Using the required sensor metadata, the ULEM uncertainty
metadata is generated as an adjustable-parameter covari-
ance matrix, ideally from the natural output of the rigorous
physical lidar model used to compute the terrain coordinates
in the point cloud. It must be provided a sufficient number
of times during a dataset collection to capture variations in
the parameter uncertainties over time. Also, the estimated
correlations among the ULEM parameter uncertainties are
required. The addition of these metadata permits calculation
of relative uncertainties between terrain points and is impor-
tant in data fusion and data adjustment algorithms (Rodarmel
et al., 2011). The process of generating the ULEM uncertainty
metadata from the sensor metadata is beyond the scope of this
paper; however the details are provided in the ULEM Imple-
mentation and Exploitation Document (NGA, 2013).
It is proposed that the vendor of the lidar hardware and
processing software supply all of this necessary metadata for
ULEM creation and that they develop the initial ULEM esti-
mates. The vendors have the insight into the full physical
sensor model to allow accurate ULEM development. Little addi-
tional burden would be imposed, since the metadata is already
available or easily derived from the sensor model used to com-
pute the point cloud ground coordinates. In supplying this
metadata, the lidar data providers need not reveal any details
of the sensor design and operation, only the resulting ULEM pa-
rameter uncertainties. However, this ULEM metadata can then
be passed through and utilized in the subsequent process-
ing architecture used by lidar practitioners. By utilizing the
CSM API, many of the details of the ULEM model exploitation
can remain hidden to the practitioner, but they can leverage
the error estimates and associated adjustments to adjustable
parameters during processing. Further, the ultimate custom-
ers of practitioners can leverage the error estimates in future
analyses of the data. This added metadata provides standard-
ized methods for downstream data adjustments. Additionally,
as the model becomes trusted and validated, it would improve
the customer’s understanding of the data accuracy by allowing
them to visualize the data accuracy spatially. Once trusted, it
could also reduce the number of check points that the custom-
ers and/or practitioners require for quality control.
Parameterization
A lidar dataset can usually be represented by a number of
collection units (CUs), with each of these units representing
a portion of data which was collected using a constant set of
collection parameters (e.g., pulse rate, sensor velocity vector),
providing consistent collection geometry. A pass, or strip,
within a collection (during which only a repeated pattern
of sensor pointing occurs) is an example of a CU . Given a CU
collected over a short period of time with minimal aircraft
dynamics, it is reasonable to assume that the sensor compo-
nent uncertainties (e.g., GPS, IMU) within the entire CU vary
so slightly that only a small subset of them are needed to
sufficiently estimate the majority of the sensor uncertainty for
the entire CU. Therefore, in this situation, the uncertainties for
all lidar points collected in a CU could be estimated using a
single set of CU -wide ULEM adjustable parameter uncertainties.
Sensor-Space ULEM CU parameters may be represented by both
constant and rate parameters, allowing for first-order polyno-
mial parameter modeling.
A list of CU polynomial parameters, based on the seven
Sensor-Space ULEM general adjustable parameters, is provided
below for each CU i:
• Δxi, Δyi, Δz i: PCS positional offsets
• θ1i, θ2i, θ3i: PCS angular offsets
• Δri: range offsets
• Δx·i, Δy·i, Δz·i: PCS positional offset rates
• θ·1i, θ·2i, θ·3i: PCS angular offset rates
• Δ· ri: range offset rate
In addition to the polynomial parameters with respect to the
PCS, there is also a need for adjustable parameters in the LCS.
These are introduced as LCS positional-offset adjustable param-
eters, ΔEi, ΔNi and ΔUi and may represent CU-wide biases.
Since the rate parameters are based on time, start and stop
timestamps are also needed for each CU. The time span per
CU is computed and used to generate scale and offset values,
so any point’s timestamp within the CU can be normalized
relative to the temporal midpoint of the CU. These normalized
548 July 2015 PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING