Pos Q L Zero Q L
Q
,
,
(
)
+
(
)
≥
T
c
(9-1)
or
Neg Q L Zero Q L
Q
,
,
(
)
+
(
)
≥
T
c
.
(9-2)
A tangent topology does not guarantee the unilateral rela-
tionship of a region to a line, as shown in Figure 2c.
2. Ipsilateral Neighbors
If both regions
Q
and
R
satisfy Equation 9 and are located
along the same side of line
L
, then they are named ipsilateral
neighbors with respect to
L
(
IPSL
-neighbors), as illustrated in
Figure 2d. Regions
Q
and
R
are not necessarily direct neigh-
bors, i.e., they share a common boundary. Multiple
IPSL
-neigh-
borhood relationships between regions
Q
and
R
are possible,
with respect to multiple correlated straight lines. Intuitively,
spatial objects are highly related with one another, i.e., seman-
tically homogeneous, if they are arranged in a semantically
meaningful configuration (e.g., a straight line). In this case, the
regions should be located on the same side of a straight line,
which is a powerful and meaningful spatial constraint.
3. Ipsilateral and Homogeneous Chain
Suppose a chain is composed by a set of regions, which is
formed as
Q
1
,
Q
2
, …,
Q
n
, in which each region in the chain is
a direct neighbor of the previous region, as illustrated in Fig-
ure 2f. If these regions exhibit some form of homogeneity and
are all
IPSL
-neighbors with respect to line
L
, then the chain
is labeled as an ipsilateral and homogeneous chain (
IPSL-H
chain).
Q
1
and
Q
n
are two nodes in this chain. The regions
in the
IPSL-H
chain are apparently highly related with one
another because the chain is constrained by similar attributes,
a specific shape, and an unbroken structure.
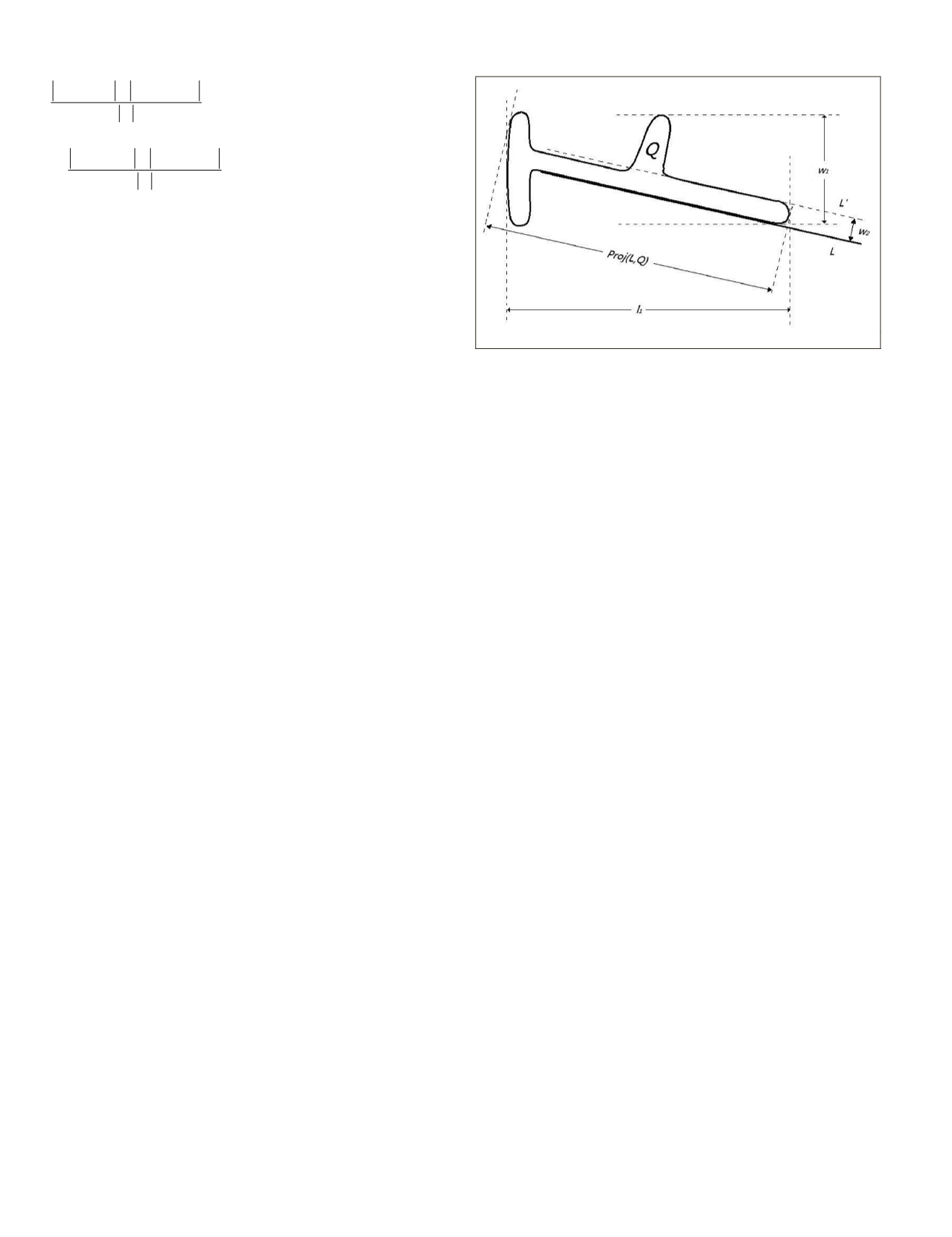
4. Line-Based Length-to-Width Ratio
The shape feature of the length-to-width ratio (
LW
) is defined
as the length (
l
) versus the width (
w
) of the minimum bound
rectangle (
MBR
) of an object, i.e.,
LW
=
l
/
w
.
(10)
Linear objects can be extracted when they have large
LW
values. However, measuring
LW
may not yield precise results
for linear but irregularly shaped objects. Thus, the line-based
length-to-width ratio (
LBLW
) is defined as follows. Suppose
we have a line
L
tangent to region
Q
, as illustrated in Figure
3. We move line
L
stepwise along its perpendicular direction
and record the position where |
ln
(
L,Q
)| declines dramati-
cally. The moving steps
w
2
is the line-based width (
LBW
) of
Q
with respect to line
L
, |
Proj
(
L,Q
)| is the line-based length
(
LBL
), and
LBLW
is defined as
LBL
versus
LBW
, as follows:
LBLW
= |
Proj
(
L,Q
)|/
w
2
.
(11)
Similar to an
IPSL
-neighborhood relationship, a region can
have multiple
LBLW
measures based on its multiple tangent
straight lines. Thus, irregular shapes can be described in ob-
jective and precise manners.
5. Region and Line Mutual Conversions
The following operations on region-and-line mutual con-
version are defined to extend spatial relationship analyses
between regions and lines.
Region-to-Line Conversion
Given a region
Q
and its contacting line set {
L
}, region-to-
line conversion is defined as the operation that extracts a
subset from {
L
} with respect to specific constraints. Typically,
extracting a subset of {
L
}, which is tangent to region
Q
and
parallel to the main axis of
Q
(if
Q
has one), may be a useful
region-to-line conversion, which is applied in the case study.
Line-to-Region Conversion
Given a straight line
L
and its contacting region set {
Q
}, line-
to-region conversion is defined as the operation that extracts
a subset from {
Q
} with respect to specific constraints. For ex-
ample, regions in the subset may be constrained to be located
on the same side of and tangent to line
L
, which indicates that
only the
IPSL
–neighbors within {
Q
} are retrieved.
Line-to-Line Conversion
Given a straight line
L
and its neighboring straight lines
{
L
*}, line-to-line conversion is defined as the operation that
extracts a subset from {
L
*} with respect to specific constraints.
The neighboring relationship between two straight lines is
defined based on they both intersect the same region. As a
typical case, the extraction of straight lines parallel to
L
is ap-
plied in the case study.
Case Study of RLPAF
Region and line primitives, as well as their mutual relation-
ships in image classification or information extraction, can
be comprehensively applied based on
RLPAF
. In this study, an
example on a road network extracted from
HSR
images is pro-
vided. In impervious surface classification from
HSR
images,
roads and buildings are sometimes difficult to distinguish
between each other when they are composed of similar mate-
rials. However, roads exhibit typical linear features, and thus,
road regions obtained by image segmentation frequently have
high
LW
s. In the
OBIA
framework, shape features (typically
measured in
LW
), along with the spectral signature, serve as
important clues in extracting linear features such as roads. In
image segmentation, however, roads are not always segment-
ed into ideal, high
LW
regions because of over-segmentation
errors and road appearance changes. A significant number of
true road regions are lost if judging is only based on high
LW
s.
In addition,
MBR
-based
LW
is limited when linear features are
irregularly shaped (e.g., with high curvatures or many forks).
Thus, we designed an
RLPAF
-based road-extraction method
(Figure 4). The method combines two processes, namely, first-
level supervised classification and second-level rule analysis.
To separate an impervious surface from other ground features,
coarse-grained supervised classification based on region
spectral signatures was initially performed. Only three classes
were specified: water body, vegetation and others, and imper-
vious surface. First-level classification helps distinguish roads
from other linear features in second-level rule-based classifi-
cation, e.g., rivers and channels. Additional features, includ-
ing region textures, shapes, or statistics on straight lines, may
Figure 3. Line-based length-to-width ratio.
152
February 2016
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


