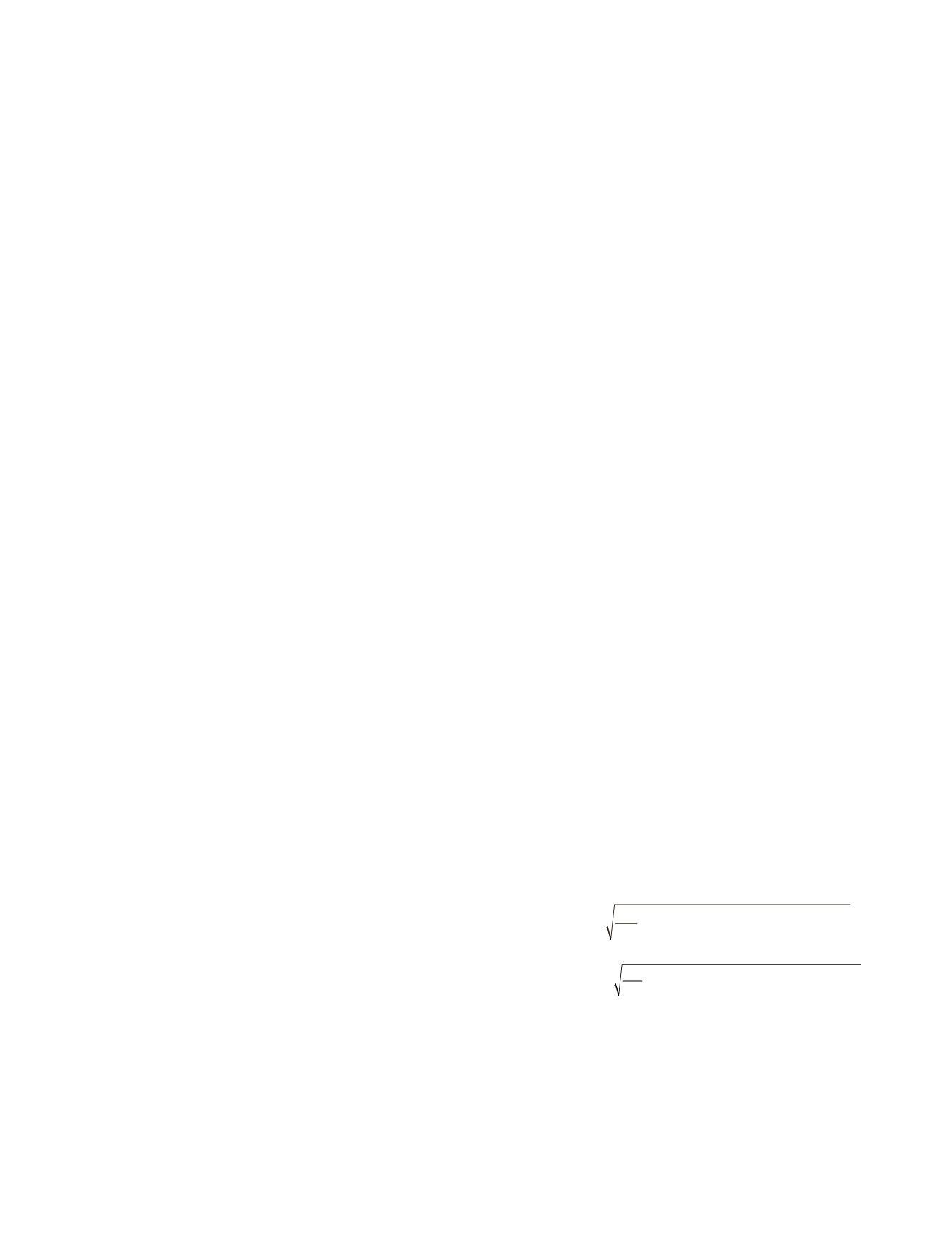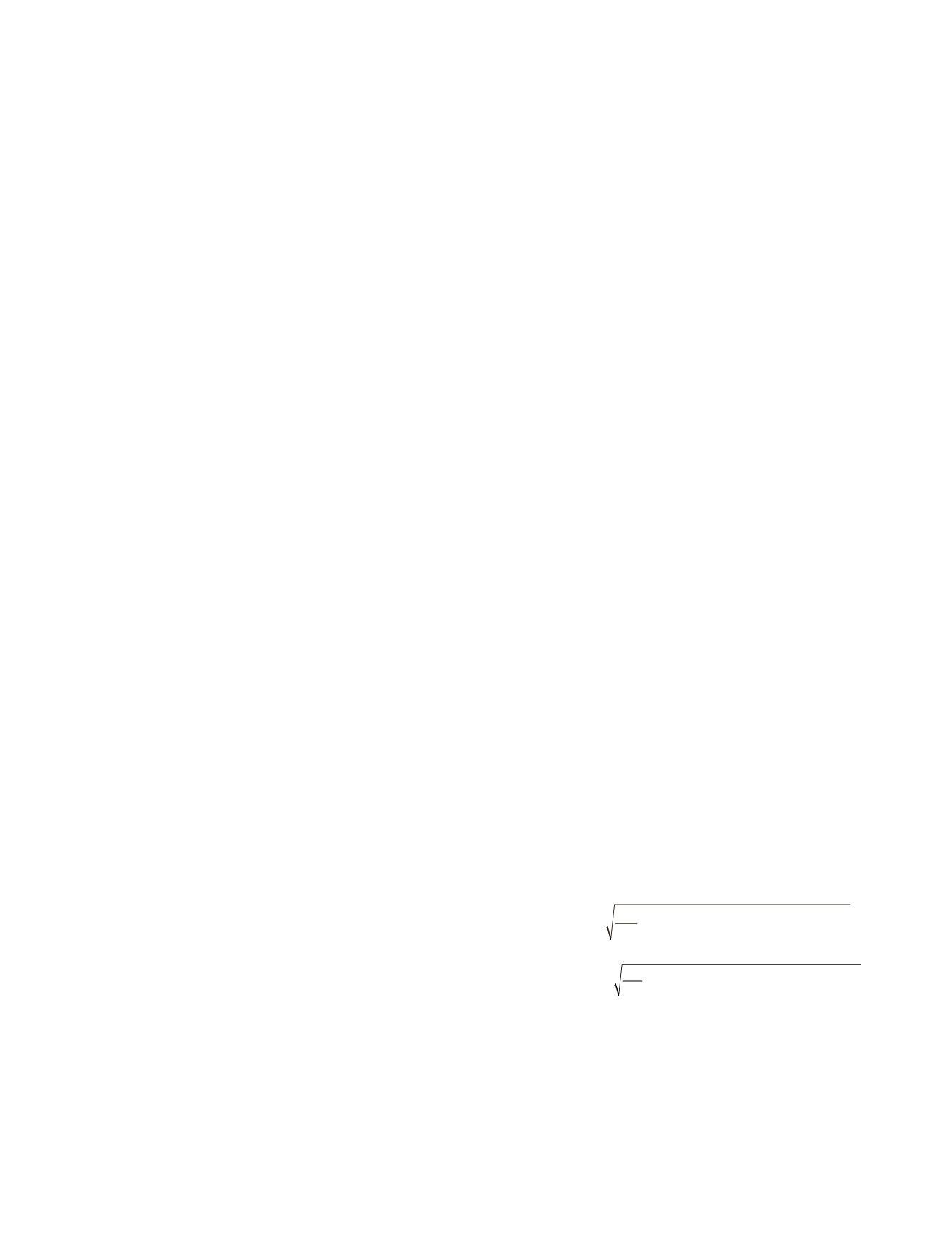
in the second Section, while incorporating all the combina-
tions of point pairs from the available image/object points. An
alternative approach to directly approximate
N
i
is to fit a plane
through the object points and consider
N
i
as the normal to this
plane. After approximating either
R
w
c
or
N
i
, the term
∑
k
i
=1
(
R
w
c
n
i
)
T
(
V
i
×
N
i
) is maximized by estimating the rotation matrix
through a quaternion-based approach similar to the introduced
methodology in the second section. For the next iterations, the
vectors
N
i
are updated as
N
i
=
R
w
c
n
i
×
V
i
in which the estimated
R
w
c
in the previous iteration is used. Therefore, the rotation
matrix
R
w
c
and the vectors
N
i
are successively updated until a
convergence criterion is met (i.e., when no significant change is
observed for the extracted rotation angles
ω
,
φ
, and
λ
from
R
w
c
).
X X
Y Y
Z Z
R
x
y
c
X X
Y Y
c
w
2
0
2 0
2
0
2
2
2
1
0
1 0
−
−
−
=
−
−
−
λ
,
Z Z
R
x
y
c
c
w
1
0
1
1
1
−
=
−
λ
(30)
X X
Y Y
Z Z
R
x
y
c
x
y
c
c
w
2
1
2 1
2
1
2
2
2
1
1
1
−
−
−
=
−
−
−
λ
λ
(31)
λ λ
1
2
2
1
2 1
2
1
2
1
2
1
0
= ⇒
−
−
−
′
=
−
−
′
X X
Y Y
Z Z
R
x x
y y
c
w
X x
=
R
c
w
(32)
After estimating the rotation matrix
R
w
c
,
the position of
the
perspective center (
X
O
,
Y
O
,
Z
O
) is derived directly through the
collinearity equations. Using the third row of the collinearity
equations (Equation 33), the scale factor can be presented as
λ
= (
Z
–
Z
O
)/
R
3
x
, where
R
1
,
R
2
, and
R
3
are the first, second, and
third rows of the rotation matrix
R
w
c
,
respectively, and
x
= [
x,y,–
c
]
T
. Multiplying the first and second rows with the derived ex-
pression for
λ
, Equation 34 can be established for every image/
object point. Considering Equation 34 for all the
n
available
image/object points, a linear system with 2
n
equations in three
unknowns (
X
O
,
Y
O
,
Z
O
)
is obtained. Therefore, the position of
the perspective center is derived by solving the linear equa-
tion system through a single-step least-squares adjustment.
λ
R
x
y
c
X X
Y Y
Z Z
c
w
−
=
−
−
−
0
0
0
(33)
R
R
R R
X
Y
Z
XR ZR
YR ZR
3
1
3
2
0
0
0
3
1
3
2
0
0
x
x
x x
x x
x x
−
−
=
−
−
(34)
In summary, the introduced projective and
DLT
approaches
in the second and third sections are limited to four or more
planar points and six or more non-planar points, respectively.
Therefore, these approaches are not suitable for applications
in which the configuration of the object points is not known
beforehand. However, these approaches are capable of deriv-
ing some of the utilized camera’s internal characteristics (i.e.,
the principal distance for the projective-based approach and
the principal point coordinates, principal distances in the
X/Y directions, and non-orthogonality for the
DLT
-based ap-
proach). The quaternion-based general method, on the other
hand, can deal with three or more points regardless of their
configuration (i.e., whether they belong to planar or non-pla-
nar object space) when using a calibrated camera.
Experimental Results
In this section, the performance of the quaternion-based pro-
jective,
DLT
, and general approaches is evaluated against other
solutions such as the non-linear
SPR
and the state-of-the-art
RP
n
P
method introduced by Li
et al
. (2012). Since the quater-
nion-based general approach is iterative, high accuracy solu-
tion is expected. Therefore, the main goal of the first experi-
ment is to investigate the accuracy of the quaternion-based
approaches for either planar or non-planar object points. For
this purpose, two datasets in planar and non-planar con-
figurations are simulated and contaminated by a normally-
distributed noise in both image and object space. In the
second experiment, the performance of the proposed methods
is evaluated for a real dataset including various oblique and
vertical image poses to challenge the
SPR
solutions. Concern-
ing the performance of the quaternion-based approaches in
terms of redundancy, both experiments are conducted with ei-
ther minimal (three or four) or redundant data. Consequently,
the minimum number of points required to achieve accurate
results can be established for all the investigated
SPR
methods.
Simulated Data
In order to evaluate the accuracy of the introduced
SPR
meth-
ods in the presence of noise, two datasets are simulated in
planar and non-planar configurations. For the planar dataset,
16 corners of a 4 × 4 grid with 20 × 15 cm cells are consid-
ered as the object points. The corresponding image points are
derived through the collinearity equations, assuming no lens
distortions and zero values for the principal point coordi-
nates. The
EOP
s are set to simulate an oblique image (
ω
= 25°,
φ
= −50°,
κ
= 105°,
X
O
= −80 cm,
Y
O
= −30 cm,
Z
O
= 70 cm) and
the principal distance (
c
) is set to 30 mm. Using the planar
dataset, the non-linear
SPR
,
RP
n
P
, projective, and quaternion-
based general approaches are tested against each other for all
the 16 points as well as minimal data of three and four points
(which have been selected as the extreme corners of the grid)
whenever applicable. The non-planar dataset is generated by
adding ±20 cm random depth to the planar dataset, and used
to compare the
DLT
and general quaternion-based approaches
with the non-linear and
RP
n
P
approaches using 16 points.
The accuracy of each
SPR
method versus noise is evalu-
ated by gradually increasing the noise level up to a standard
deviation of ±20 pixel to the image point coordinates and up
to ±1 cm to the object point coordinates, and recording the es-
timated
EOP
s from such experiments. For a given noise level,
each
SPR
method is run
m
= 100 times, and the rotation and
translation recovery errors are evaluated using the
RMSE
of the
differences between the estimated and true
EOP
s which are
used in the simulation. The rotation and translation recovery
errors are derived using Equations 35 and 36, where (
ω
i
,
φ
i
,
κ
i
) are the rotation angles and (
X
i
O
,
Y
i
O
,
Z
i
O
) are the translation
parameters estimated from the
i
th
iteration
.
Rotation error
=
−
(
)
+ −
(
)
+ −
(
)
=
∑
1
3
2
1
2
2
m
i
i
m
i
i
ω ω φ φ κ κ
(35)
Translation error
=
−
(
)
+ −
(
)
+ −
(
)
=
∑
1
3
2
1
2
2
m
X X Y Y Z Z
o
i
o
i
m
o
i
o
o
i
o
(36)
For the planar dataset, the rotation and translation re-
covery errors associated with each
SPR
method using three,
four, and 16 points are presented in Figure 3, which shows
that the quaternion-based general approach is robust to noise
for minimal and redundant data. Figure 3a shows that the
quaternion-based general approach is identical to the non-lin-
ear method using three points. Figure 3b and Figure 3c depict
the accuracy of each
SPR
method using four and 16 points,
respectively. According to these figures, the quaternion-based
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
March 2015
213