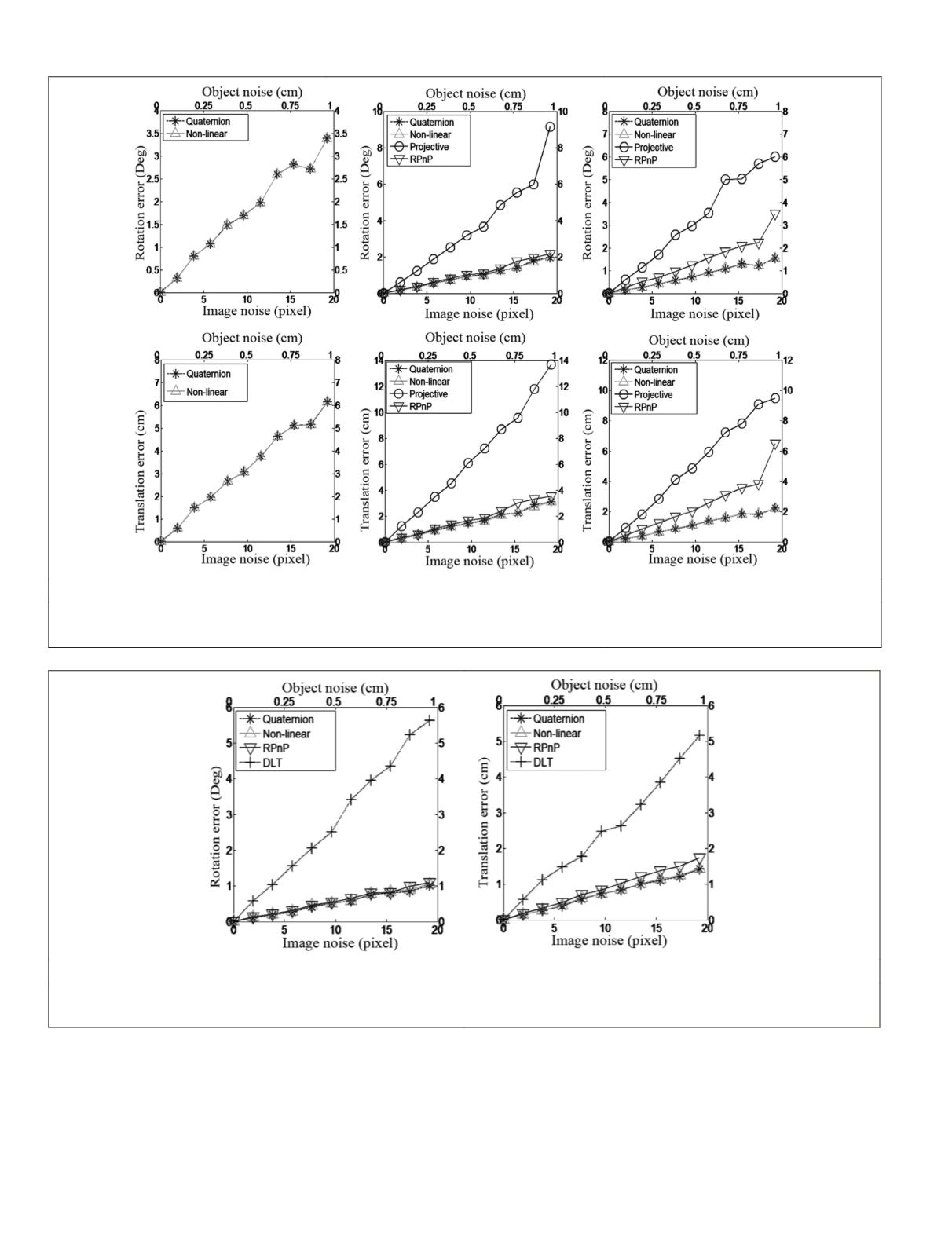
general approach is more accurate than the projective method
and remains stable and close to the non-linear
SPR
method.
Although the
RP
n
P
shows close performance to the non-linear
SPR
using four points, it performs slightly worse when dealing
with 16 points. Therefore, the performance of the quaternion-
based general approach proves its robustness when dealing
with noisy redundant data.
Figure 4 depicts the results obtained by executing the dif-
ferent
SPR
methods on the simulated non-planar dataset using
16 points. According to the presented rotation and translation
recovery errors in Figure 4, the performance of the quaterni-
on-based general approach is almost identical to the non-lin-
ear method and is far superior to the
DLT
method. In addition
to the quaternion-based general approach, the accuracy of
(a)
(b)
(c)
Figure 3. Rotation and translation recovery errors for the different SPR methods against image and object space noise for the planar
dataset: (a) three points, (b) four points, and (c) 16 points.
(a)
(b)
Figure 4. (a) rotation, and (b) translation recovery errors for the different SPR methods against image and object space noise for the non-
planar dataset.
214
March 2015
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


