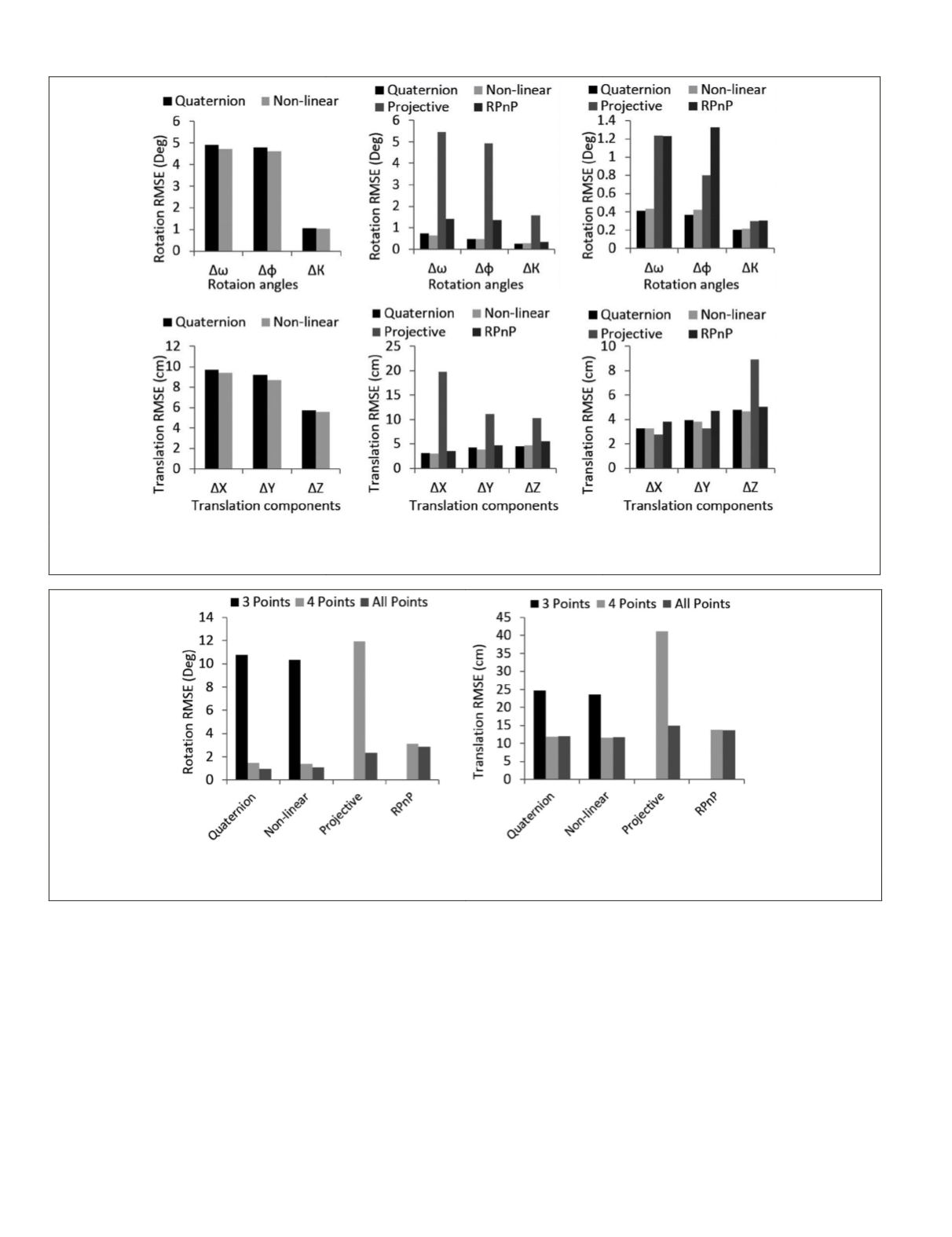
four points, but shows better accuracy when dealing with
redundant data.
As mentioned earlier, the quaternion-based general ap-
proach works with three or more points. However, four points
are enough to achieve accurate results. Figure 8 is a rearrange-
ment of the results in Figure 7, which shows the summation
of the rotation angles recovery errors (Figure 8a) and the
translation components recovery errors (Figure 8b) for each
SPR
method. According to Figure 8, the quaternion-based
general approach shows significant improvement using four
points compared to the use of three points, but not too much
using all the points. The non-linear and
RP
n
P
SPR
methods
show similar behaviour to the quaternion-based general
approach (i.e., they require four points for high accuracy).
However, the projective-based approach requires more than
four points to achieve reasonable results.
Conclusions and Recommendations for Future Work
In this paper, three quaternion-based approaches to solve
the
SPR
problem are presented. The first two are based on the
manipulation of the projective and
DLT
coefficients to directly
estimate the rotation matrix following the evaluation of the
perspective center coordinates. In addition to the pose param-
eters, the projective-based approach recovers the principal
distance and the
DLT
estimates the principal point coordi-
nates, principal distances in the X/Y directions, and non-
orthogonality. The third one (the quaternion-based general
approach) iteratively solves for the rotation matrix by enforc-
ing a simple geometric constraint, and then directly derives
the translation by a linear approach. These methods do not
require user-defined approximate values for the
EOP
s. How-
ever, the third one works with three or more points without
any change in the implementation procedure for either planar
(a)
(b)
(c)
Figure 7. RMSE for the different SPR methods using the real dataset: (a) three points, (b) four points, and (c) all points.
(a)
(b)
Figure 8. Accuracy of the different
spr
methods versus the number of utilized points: (a) Rotation
rmse
(deg), and (b) Translation
rmse
(cm).
216
March 2015
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


