regularization is proposed to improve classification accuracy.
However, the
CSC
scheme cannot exploit the similarities and
differences among neighboring pixels. Following the method
of Zhao, Fei-Fei, and Xing (2011), a smoothness-regularization
term is introduced into the
CSC
method to effectively improve
HSI
-classification performance. Next, the details of the
CSC
method, the
CSCSR
formulation, the optimization algorithm,
and the classification steps are given.
Collaborative Sparse Coding
The
CSC
for
HSI
classification is based on two intuitive as-
sumptions. The first one is that a hyperspectral pixel is more
likely to be sparsely represented by a linear combination of a
few atoms from a structured dictionary. The other assumption
is that neighboring
HSI
pixels are more likely to belong to the
same class. Thus, based on these assumptions, a collaborative
framework is created for sparse coding of neighboring pixels
in order to improve
HSI
-classification performance.
Specifically, an
HSI
patch is represented as
Y
= [
y
1
, …,
y
k
]
∈
R
b×k
, where
k
is the
patch and
b
is the number of spectr
the central patch pixel to be classifi
shown in Figure 5, where the center
cated by a red point. There are eight neighboring pixels that
are considered in the classification process.
Let
D
= [
D
1
,
D
2
,…,
D
L
]
∈
R
b×m
be the structured all-
class dictionary, where
L
is the number of classes. Let
D
i
= [
d
1
i
,
d
2
i
,…,
d
i
n
i
]
∈
R
b×n
i
denote the subdictionary of class
i
whose vectors are composed of training samples of class
i
, where
n
i
is the number of training samples in
D
i
and
n
1
+
n
2
+ … +
n
L
=
m
. An example of a structured dictionary is
shown in Figure 6.
Based on this mathematical notation,
CSC
can be formu-
lated as the following convex optimization problem:
y D
−
+
min
,
α
α
α
j
j
j
j
j
1
2
2
2
1
1
1
=
∑
λ
k
(8)
where the subscript
j
runs through {1, 2, …,
k
},
λ
1
is a regular-
ization parameter, and
Ψ
= [
α
1
, …,
α
k
]
∈
R
m×k
is a sparse-coding
matrix. The
CSC
method can achieve better classification per-
formance than the
SC
method, as shown under Experimental
Results and Analysis. However, regardless of whether a cen-
tral-patch pixel and its neighbors share the same class or not,
those neighbors contribute equally to the
HSI
-classification
process, leading possibly to wrong classification. To improve
classification accuracy, a
CSCSR
scheme is proposed. This
scheme adjusts the contribution of a neighbor according to
class mismatch: while our scheme weakens the contributions
of neighboring pixels having classes that are different from
the class of
y
c
, it strengthens the contributions of neighboring
pixels having the same class as
y
c
.
Adding Smoothing Regularization Through CSCSR
The aforementioned
CSCSR HSI
-classification scheme is based on
a point-wise selection of small image patches with a fixed size
in the neighborhood of the testing pixel. Here, an additional
smoothness-regularization term is introduced into the
CSC
for-
mulation (Equation 8), leading to the following problem:
+
−
λ
λ
n
,
j
j
y D
−
+
mi
α
α
α
α
α
j
j
j
j
j
1
2
2
2
1
1
2
2
2
1
=
∑
ω
k
(9)
eter. There are three terms in this
plays a different role.
Representation error:
The first term,
1
2
2
2
1
y D
j
j
j
−
=
∑
α
k
, is the
sparse representation error. For a testing hyperspectral pixel,
this term should be small due to the assumption that the giv-
en dictionary accurately represents knowledge in the training
data. That is, each testing pixel can be represented as
y
j
≈
D
α
j
.
Figure 7a shows a plot of the measured spectral profile of a
Figure 5. An example of a hyperspectral image patch,
centered at
y
c
.
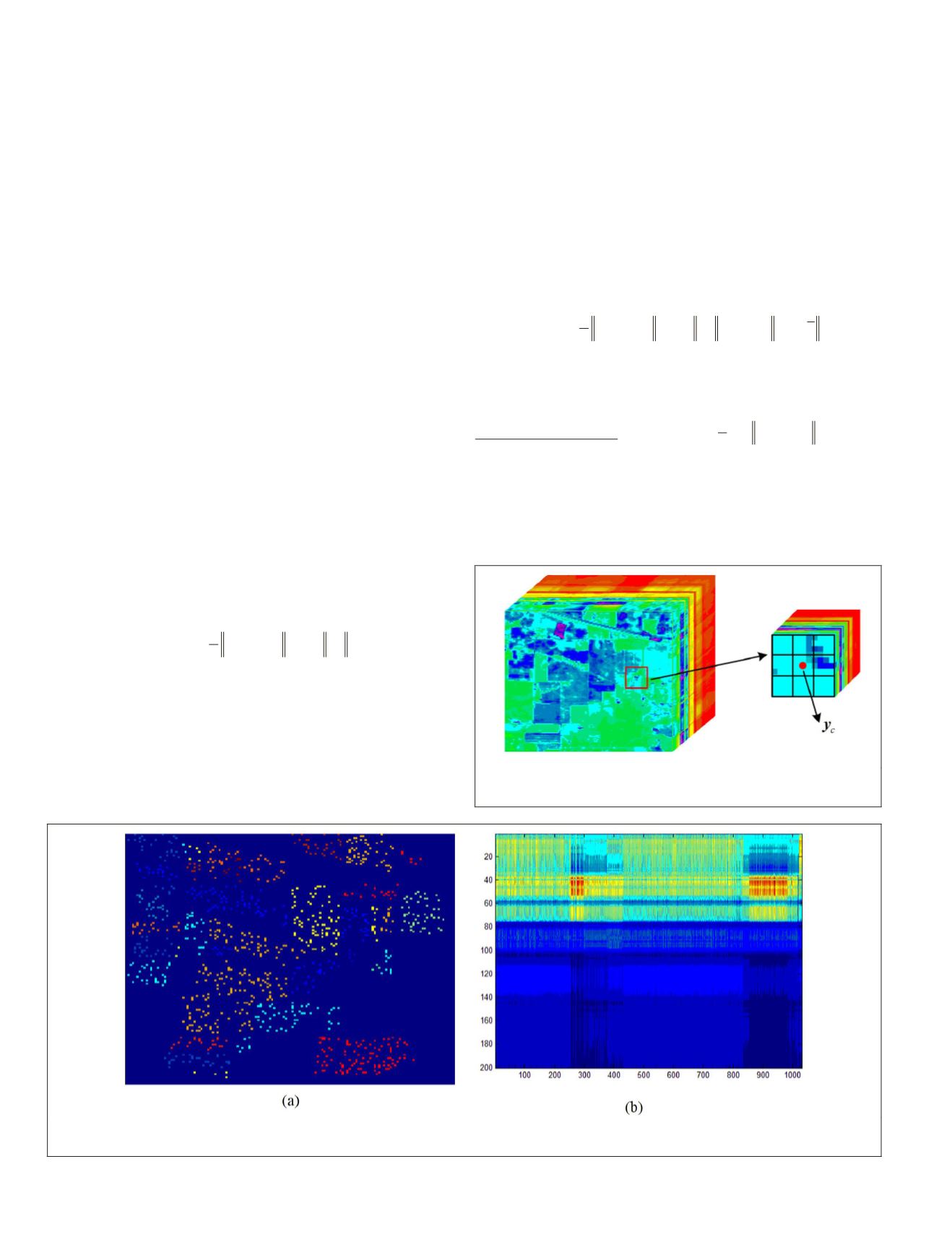
Figure 6. A sample structured dictionary: (a) training samples (points denote pixels extracted from the Indian Pines
hyperspectral-image data set), and (b) a structured dictionary with 1034 atoms and 200 bands.
662
September 2019
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


