e
i
j
i j
i
j
=
−
=
∑
y D
ˆ ,
α
2
2
1
k
(12)
where
D
i
is the subdictionary associated with class
i
and ˆ
α
i
j
is the subset of the sparse representation
vector ˆ
α
j
associated with class
i
. The output class is
the one that achieves the minimum overall repre-
sentation error:
label(
y
c
) = arg min{
e
i
}.
(13)
Algorithm 2 summarizes the steps of the
CSCSR
-
based
HSI
-classification scheme.
Experimental Results and Analysis
To validate the effectiveness of the proposed
CSCSR
ess its performance in comparison
s, we performed experiments on
HSI
was preprocessed using two it-
rediction (C. Chen
et al.
2014). For
Equation 6, the following parameter settings were
used:
n
s
= 9,
s
= 80, and
γ
= 2. To find the optimal
weighting parameters
λ
1
and
λ
2
of the
CSCSR
scheme
in Equation 9, a natural solution was to alternate
between these two parameters, changing one while
fixing the other. Specifically, to find
λ
1
, the param-
eter
λ
2
was set to zero. When
λ
1
with the best accu-
racy was found,
λ
1
was fixed to search for
λ
2
. This
alternating pattern was repeated until the accuracy
converged to a local optimum, and hence the final
values of the two parameters were determined. In
the classification stage, 10% of the samples from
each class were randomly picked up for training and the re-
maining 90% of the samples were used for testing. The train-
ing samples were used to form the dictionary in the sparse-
signal model. The performance of the proposed scheme was
compared against state-of-the-art classifiers, namely support
vector machines (Camps-Valls and Bruzzone 2005; Melgani
and Bruzzone 2004), collaborative representation (L. Zhang
et
al.
2011), nearest regularized subspace (Li
et al.
2014), joint
collaborative representation (Li
et al.
2014), kernel collabora-
tive representation with Tikhonov regularization and compos-
ite kernel (W. Li
et al.
2015), orthogonal matching pursuit (Y.
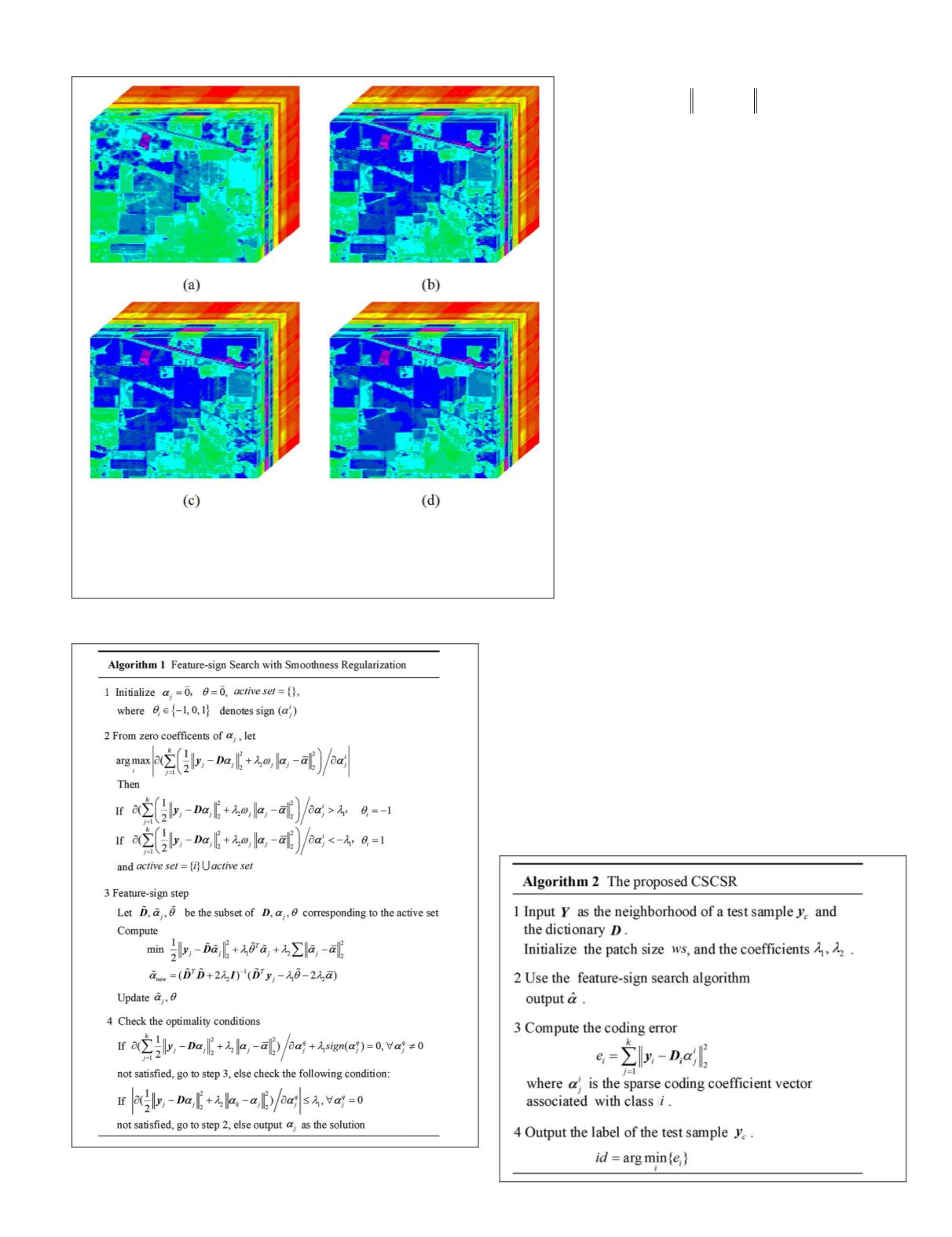
Figure 10. Hyperspectral-image reconstruction example: (a) the
input image, (b) the reconstructed image using sparse coding, (c) the
reconstructed image using collaborative sparse coding, and (d) the
reconstructed image using collaborative sparse coding with smoothness
regularization.
Algorithm 1. Feature-sign search with smoothness
regularization.
Algorithm 2. The proposed collaborative sparse coding with
smoothness regularization.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
September 2019
665


