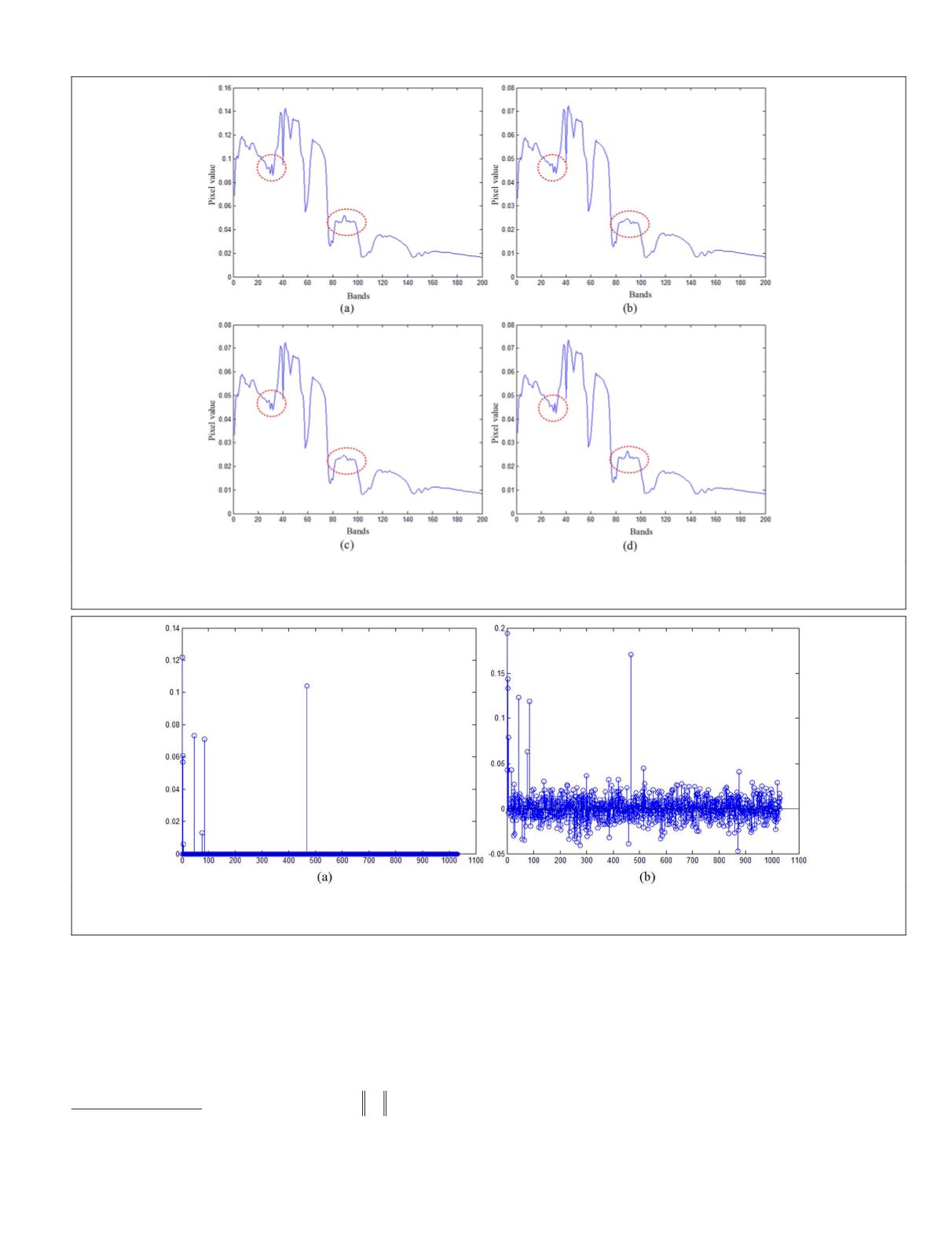
raw pixel in a sample
HSI
. The reconstructed spectral pro-
files of the same pixel using
SC
,
CSC
, and
CSCSR
methods are
shown in Figure 7b–7d, respectively. It can be seen that the
pixel spectral profile obtained by
CSCSR
is more similar to the
original profile than those generated by the
SC
and
CSC
meth-
ods. Two particular curve segments (encircled by red dotted
lines) support this conclusion. Therefore, our proposed
CSCSR
method can obtain the minimum reconstruction error.
Sparsity constraint:
The second term,
λ
1
1
1
α
j
j
=
∑
k
, is the
l
1
-norm sparsity constraint. Enforcing sparsity in sparse coding
is necessary due to the fact that the dictionary
D
is redundant.
Given a testing pixel
y
c
, the neighboring pixels
Y
and sparse
coefficient matrix
Ψ
can be obtained. If
y
j
belongs to the
i
th
class, where
α
j
= [
α
1
j
; …
α
i
j
; …;
α
L
j
], the approximation
y
j
≈
D
i
α
i
j
usually works well—that is, most of the entries of
α
h
j
,
h
≠
i
, are
nearly zero—and
α
i
j
has coefficients of significant magnitudes.
The sparse representation of
y
j
over the dictionary
D
is natu-
rally discriminative and thus can find the class of
y
j
(Wright
et al.
2009). To show the importance of imposing sparsity,
the sparsity-constraint term is removed from Equation 9 and
the resulting representation vector is observed. As shown in
Figure 8, if there is no sparsity constraint, the representation
vector can be too dense to infer the correct class.
Figure 7. Original and reconstructed hyperspectral pixel intensity profiles for the Indian Pines hyperspectral-image data set:
(a) original profile, (b) reconstructed profile using sparse coding, (c) reconstructed profile using collaborative sparse coding,
and (d) reconstructed profile using collaborative sparse coding with smoothness regularization.
Figure 8. Dictionary-based representation of a hyperspectral-image pixel using collaborative sparse coding with smoothness
regularization: (a) sparse representation with the sparsity constraint, and (b) sparse representation when the sparsity
constraint is absent.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
September 2019
663


