proposed to acquire specific land cover reflectance for further
fusion (Xie
et al.
2016). To deal with the complex surface
changes, Huang and Zhang (2014) proposed the unmixing-
based spatiotemporal reflectance fusion model (U-STFM),
which obviously improved the accuracy of capturing land-
cover-type changes. Zhu
et al.
(2016) proposed a flexible
spatial-temporal data fusion (
FSDAF
) algorithm with minimum
input data, which is suitable for heterogeneous landscape and
land-cover-type changes.
In the learning based methods, based on sparse representa-
tion theory, Huang and Song established the corresponding
relationship between high- and low-resolution images to
predict the high-resolution images of another period, which
shows advantages in forecasting images with phenological
changes and land-cover type changes (Huang and Song 2012).
In order to reduce the use of input data, one pair of images are
used for dictionary learning and the prediction process is im-
plemented in a two-stage framework (Song and Huang 2013).
However, the algorithm based on sparse representation brings
certain complexity and instability. In recent years, some
scholars have introduced deep learning algorithm into the
field of spatiotemporal fusion. Song
et al.
(2018) established a
novel spatiotemporal fusion using deep convolutional neural
network (
STFDCNN
), which can effectively extract and express
information in large-scale remote sensing data, and achieve
satisfactory performance. Tan
et al.
(2018) proposed a new
deep convolutional spatiotemporal fusion network (
DCSTFN
),
which fully uses convolutional neural networks to obtain
high spatial-temporal resolution images. The results show
that this method has higher fusion precision and is more ro-
bust than the traditional spatiotemporal fusion algorithm.
The above methods are mostly based on pixel-by-pixel
processing, which will make the fusion of each fine-coarse
resolution image pair take a long time to predict results. In
practical application, when long time series images are need-
ed, these methods will be very time-consuming. In contrast,
learning-based methods spend more time in training process,
but need much less time in forecasting. At present, deep
learning has achieved excellent performance in computer
vision (Zhang
et al.
2017; Kim, Lee, and Lee 2016; Tong
et al.
2017; Ledig
et al.
2017; Girshick
et al.
2014; Ren
et al.
2015;
Wang
et al.
2017). More and more deep l
works have been introduced into remote
Zhang, and Du 2016; Zhu
et al.
2017). F
tiotemporal fusion methods based on de
recently show their potential to process data in batches and
detect texture features of objects (Song
et al.
2018).
Given the aforementioned concerns, the objective of this
research is to develop an effective spatiotemporal fusion
algorithm. In order to reduce the impact of large resolution
differences between input data on the algorithm, a two-stage
fusion algorithm is proposed. In the first stage, the input data
is firstly preprocessed to the transitional resolution, and then
a linear interpolation model is used to fuse the input data for
initial fusion. In the second stage, residual dense network is
introduced to reconstruct the preliminary fusion results to
obtain the final fusion results with the same resolution to the
fine-resolution image. The main contributions of this paper
are as follows: 1) The linear interpolation model effectively
integrates the spatial and spectral information from the pre-
processed input data to produce more accurate transitional
fused results, 2) the introduced residual dense network fully
extracts and uses the hierarchical features from transitional
fused data, and can effectively establish the mapping from
preliminary images to real fine-resolution images for recon-
struction, thus, more detailed spatial structure of the image
can be captured in the fusion results, and 3) the model can be
saved and reused after training, which improves data process-
ing efficiency when acquiring long-term sequence images in
the same study area.
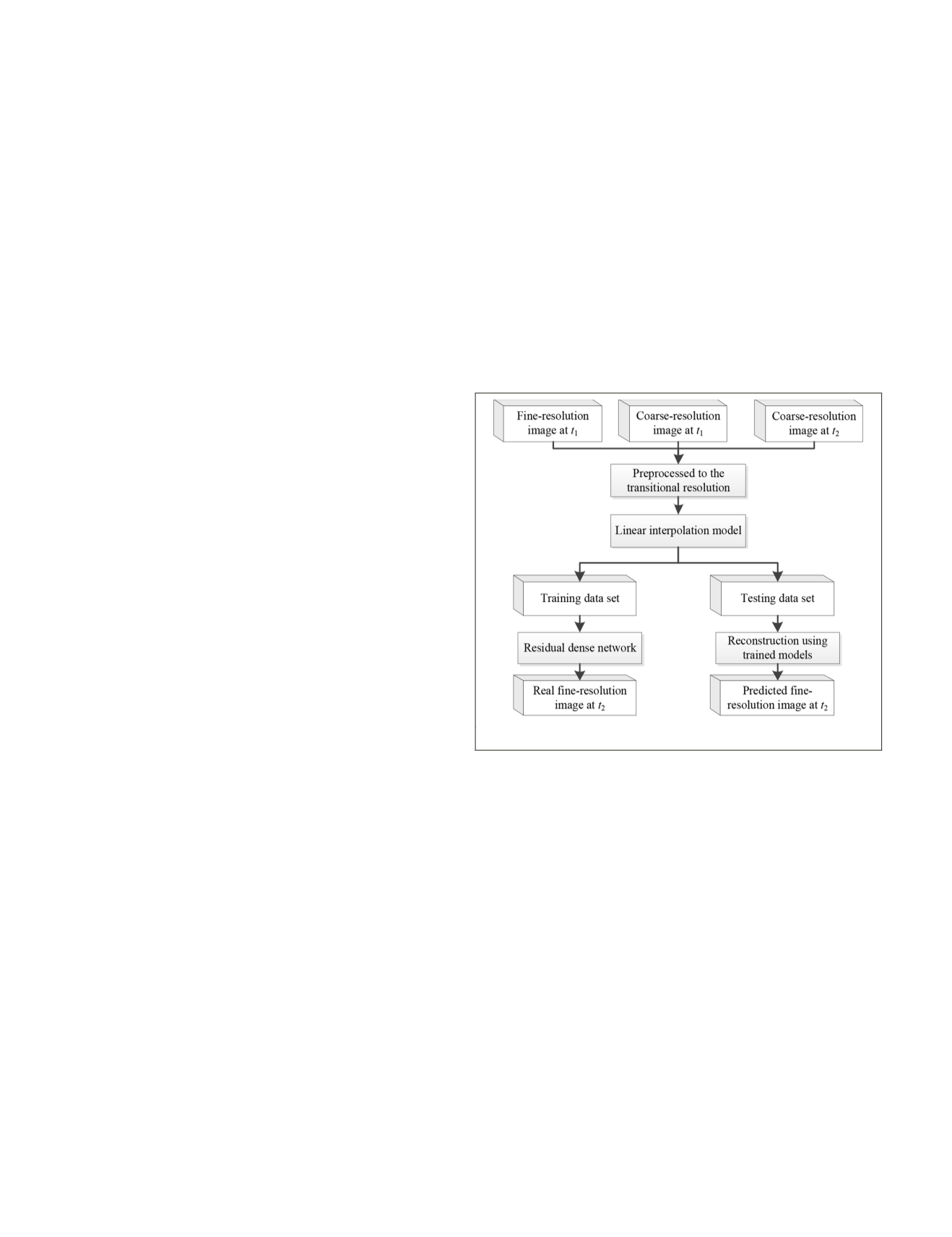
Methodology
In this paper, a two-stage spatiotemporal fusion method is pro-
posed for remote sensing images. Here, the data sets of Land-
sat and
MODIS
are used to demonstrate the proposed fusion
method. (however, other remote sensing images such as Senti-
nel-3 and Sentinel-2 can also be adopted in our method). One
Landsat-
MODIS
image pair and a
MODIS
image on the prediction
date are used as input data to predict the Landsat image on the
prediction date. Considering the large spatial resolution differ-
ence between Landsat image and
MODIS
image, the method is
implemented in two stage. In the first stage, the Landsat image
is downsampled to the transitional resolution, and the
MODIS
image is upsampled to the same resolution. Then a linear
interpolation model is used to fuse the preprocessed input
images for obtaining preliminary fusion results. In the second
stage, the residual model is introduced to reconstruct the
preliminary fusion results to acquire the Landsat image on the
prediction date. The main idea and flowchart of the proposed
method are demonstrated in Figure 1.
f the proposed method.
l
The difference between the high and low resolution of Land-
sat-
MODIS
data sets used in this paper is 20 times. In this case,
we consider the fusion of 10 times resolution difference first.
The Landsat data is reduced by 2 times for the spatial resolu-
tion, and the
MODIS
data is upsampled to the same resolu-
tion with the resampled Landsat data. A linear interpolation
model commonly used for pan-sharpening is used to fuse the
resampled Landsat and
MODIS
data (Vivone
et al.
2015). The
model is given as follows:
ˆ
,
,
,
,
F C
F -C
2,
2
2
1
2
1
b
b b b b
g
↓
↓
= ′ +
′
(
)
(1)
where F
1
2
,b
↓
represents the b band Landsat image at time t1 af-
ter reducing the resolution by 2 times. C
1
,b
′
and C
2
,b
′
are the
upsampled image with the same resolution to F
1
2
,b
↓
at t1 and t2
using bicubic interpolation method. The linear interpolation
model integrates the spatial information of the high-resolution
image and spectral information of the low-resolution image
to produce the fused results F
1
2
,b
↓
. In Equation 1, the injection
gain
g
b
is defined, for b band, as
908
December 2019
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


