topographic maps, which correspond to root mean square
errors (
RMSE
) of less than 25 and 6 m for planar and vertical,
respectively (People’s Republic of China National Standard,
2008). Thus, a systematic analysis and experimental verifica-
tion of the image accuracy of
ZY-3
satellite without
GCP
s is
needed. However, the research on the geometric accuracy of
ZY-3
images and other
HRSI
s mentioned above, mainly focused
on the influences and evaluation of the geometric accuracy
of image using given on-orbit calibration methods, different
block adjustment models, or varying geometrical rectification
methods. Meanwhile, these researches failed to investigate
precisely the main error sources influencing geometric accu-
racy of images and the error propagation model based on the
geometric characteristics of various satellite sensors, and did
not further analyze and evaluate the geometric accuracy of the
satellite images quantitatively and theoretically. Moreover, the
geometric accuracy of the
ZY-3
satellite images has rarely been
systematically studied and verified without
GCP
s.
This paper gives a brief introduction of several key pro-
cessing steps to ensure geometric accuracy in
ZY-3
satellite
image production. The main error sources influencing the
geometric positioning accuracy of the
ZY-3
satellite images
were also studied. By analyzing the error propagation model
of these error sources, the planar and vertical accuracy
estimation models of the
ZY-3
satellite images were deduced.
According to the model mentioned above, the theoretical
geometric positioning accuracy for the
ZY-3
satellite images
without using
GCP
s was calculated. Finally, to testify the cor-
rectness of the accuracy estimation models, a large quantity
of
ZY-3
images were used to conduct the geometric accuracy
verification experiment without using
GCP
s.
Accuracy Analysis
Error Sources for the Geometric Accuracy
The geometric positioning accuracy of the
ZY-3
satellite imagery
depends on the geometric accuracy of the rigorous geometry
sensor model. Neglecting the effect of atmospheric refraction,
the rigorous geometry sensor model for the
ZY-3
satellite image
is established as follows (Pan
et al.,
2013; Tang
et al.,
2012):
X
Y
Z
X t
Y t
Z t
mR
Wgs
Gps
Gps
Gps
J
=
+
84
2000
( )
( )
( )
Wgs
Star
J
Star
Body T
x
y
z
x
y
t R t R
D
D
D
d
d
84
2000
( )
( ) (
)
+
d
R
tg
tg
f
z
Camera
Body
Y
X
+
−
−
( )
( )
ψ
ψ
1
•
•
•
•
•
(1)
where [
X Y Z
]
T
Wgs
84
are the three-dimensional (3D) Cartesian
coordinates of an object space point corresponding to the im-
age point in the
WGS
84 frame, whose accuracy, which depends
on the combined effect of all components on the right side
of the equation, corresponds to the geometric positioning ac-
curacy of the satellite imagery;
t
represents the imaging time of
the scanning lines of the
TDI CCD
linear array, provided by the
satellite for each line of image. The orbit and attitude measure-
ment data for each line of image can be accurately interpolated
according to the imaging time. Thus, the time synchronization
error of the on-board equipments (cameras, global positioning
system [
GPS
] receiver, star trackers, etc.) will affect the final
positioning accuracy of model. [
X
gps
(
t
)
Y
gps
(
t
)
Z
gps
(
t
)]
T
refer to
the coordinates of the
GPS
antenna phase center at imaging
time
t
in the
WGS
84 frame, measured by the
GPS
receiver on
the satellite, with an accuracy affected by the orbit measure-
ment error.
R
J2000
Star
(
t
) represents the rotation matrix for convert-
ing the attitude determination reference coordinate system to
the J2000 coordinate system at imaging time
t
and is acquired
by the star tracker and gyro on the satellite, with an accuracy
affected by the attitude measurement error. [
D
x
D
y
D
z
]
T
are
the three offset vectors of the
GPS
phase center in the satellite
coordinates, [
d
x
d
y
d
z
]
T
define the transformation between the
camera frame and the satellite platform,
R
Body
Star
expresses the co-
ordinate rotation relationship between the star tracker and the
satellite system, and
R
Body
Camera
represents the installation matrix
of the camera on the satellite platform. The four components
denote the geometric relationship between the payload and the
measurement equipments on the satellite, and their accuracy
is mainly influenced by equipment installation errors.
f
is the
focal length of camera, and (
ψ
X
,
ψ
Y
) are the look angle of every
detector on the
CCD
linear array. These two components reflect
the internal geometric relationship of the camera and their
accuracy depends on the distortion error of the camera.
R
Wgs
84
J
2000
(
t
)
refers to the rotation matrix for converting the J2000 coordinate
system to the
WGS
84 geocentric coordinate system at imaging
time
t
and can be accurately obtained externally, showing less
influence on the geometric positioning accuracy;
m
denotes
the scaling factor. According to the analysis above, the main
factors influencing the stereo mapping accuracy of
ZY-3
satellite
images include time synchronization errors, attitude, and orbit
measurements errors (including systematic errors and random
errors), and on-board equipment (camera, star tracker, and
GPS
)
installation errors, and camera distortion errors.
Measures to Guaranty the Geometric Accuracy
On-orbit Geometric Calibration
The impulsion during satellite launching and the on-orbit
variations of the physical environment during operation
change the imaging parameters of the satellite after a very
strict laboratory calibration before satellite launch. In addi-
tion, there are systematic biases in the satellite attitude and
orbit measurements. Periodical on-orbit geometric calibration
is then necessary to reduce or eliminate the systematic errors
related with the payload installation, measurements of at-
titude and orbit, and camera distortion, thereby improving the
geometric accuracy of the satellite imagery (Leprince
et al.,
2008; Poli and Toutin, 2012).
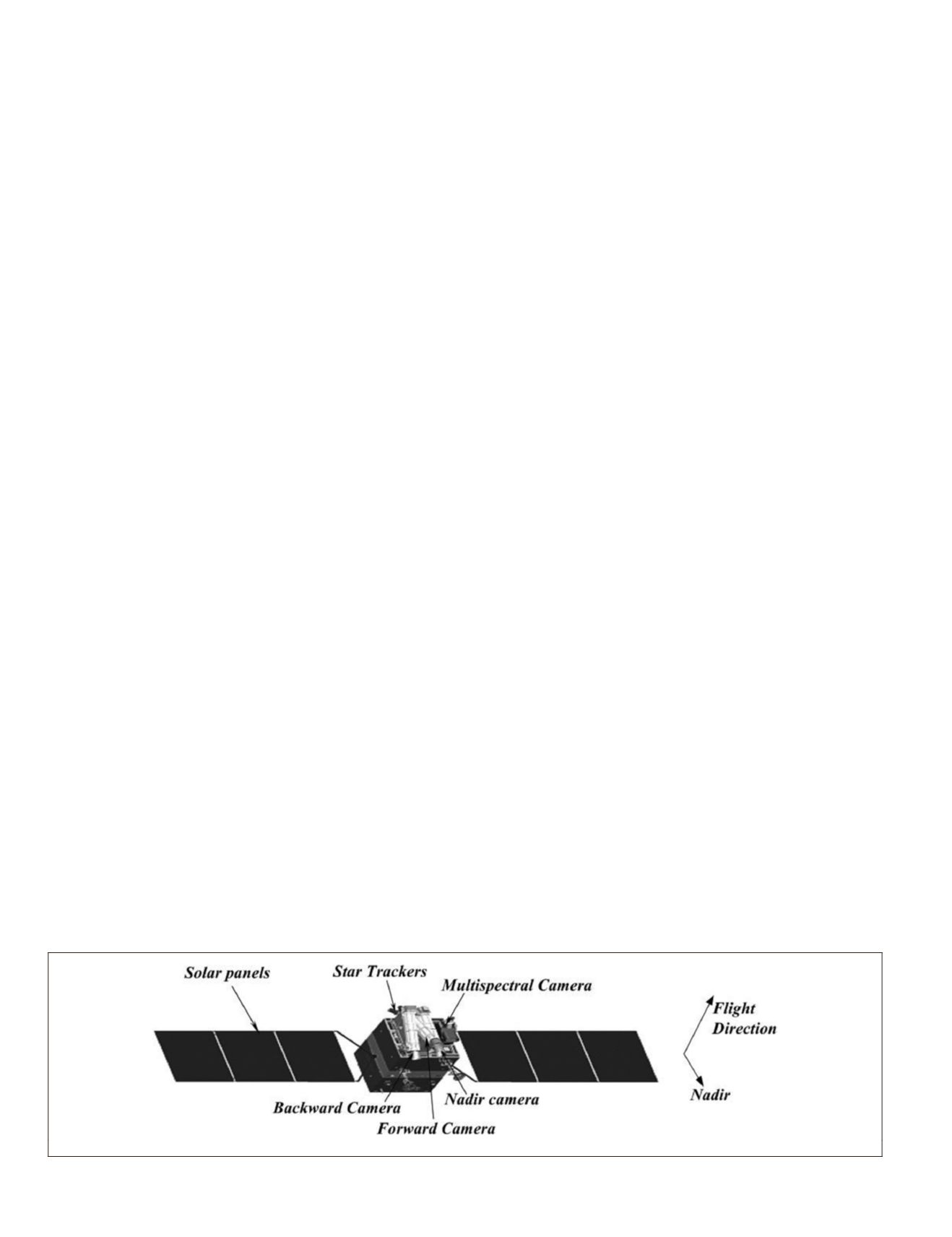
Figure 1. Schematic of the ZY-3 satellite.
928
December 2015
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


