In this paper, feature descriptions are matched using the
ratio test of nearest neighbors proposed in Lowe (2004). If the
ratio of a match is lower than a fixed threshold (the closest
neighbour is relatively much closer than the second clos-
est one), we then consider it is a reliable match. It should
be noted that the proposed method eliminates the distortion
effects arising from equirectangular projection, nevertheless,
inherent problems in planar image matching such as repeated
patterns and occlusions may still reduce the matching effec-
tiveness. Thus, a refining process such as RANSAC (Raguram
2013) or outlier detection based on least squares regression
(Johansen and Nielsen, 2014) is indispensable to remove
errors before further applications. The latter algorithm is ap-
plied in this study.
Validation
In this paper, we use spherical panoramic images as input
instead of parabolic ones and assume cameras have been cali-
brated. We first evaluate the geometric rectification for the im-
age distortion caused by equirectangular projection and then
perform feature matching under different levels of distortion.
To evaluate the validity of the proposed strategy for enhanc-
ing the spherical matching performance, we compare our
results with those obtained from existing
SIFT
- and
SURF
-based
methods. Furthermore, we show the possibility for match-
ing between planar and spherical panoramic images as well
as for establishing 2D-to-3D correspondence with lidar data,
highlighting the potential for further exploitation of imagery.
Finally, we assess the effectiveness of the proposed method in
pose estimation of a spherical image sequence.
Evaluation of Spherical Image Matching
As described above, the equirectangular projection of a
spherical panoramic image causes substantial geometric
distortion in areas close to the poles, and this reduces the
performance of feature matching since the local appearances
become dissimilar. In this case,
we collect 48 images with Nikon
P1000 and stitch them to generate
a 2048 × 1024 panoramic image,
as shown in Figure 4. To gain an
insight into the validity of the rec-
tification, we form a sphere based
on the panoramic image and rotate
the spherical coordinate system
to generate two equirectangular
images with distinct distortion as
shown in Table 1(a). Feature points
are detected by
SURF
while the
black areas are imaging blind spots.
The circular regions specifically
mark three corresponding points in
both panoramic images. Table 1(b)
shows the magnified image patches
of these point pairs and the results
after the rectification.
The circular regions, which are
located at the most distorted areas,
are geometrically correct after recti-
fication and reveal near perspective
views. Notably, the feature point
in the region B of image 2 of Table
1 can still be rectified even though
it is located very close to the north
pole of the sphere. Nevertheless,
description of a feature will only
be founded on the available data
around the point. In case that a
feature description cannot be gen-
erated due to insufficient informa-
tion, the feature point will be excluded from the subsequent
matching process.
To further explore the impacts of the rectified feature
matching towards differing degrees of image distortion,
we generate a set of equirectangular images by rotating the
spherical coordinate system along the y-axis with
ω
,
ω
∈
{
π
3
,
π
2
,
2
3
π
,
π
,
4
3
π
,
3
2
π
,
5
3
π
}, and each rotated
image is matched with the un-rotated one. For a fair evalu-
ation,
SIFT
(Lowe 2004), Spherical
SIFT
(Cruz-Mota
et al
.,
2012),
PR+SIFT
(Taira
et al
., 2015),
SURF
(Bay
et al
., 2006), and
PR+
SURF
(replacing the role of
SIFT
in
PR+SIFT
with
SURF
),
and the proposed methods that combined with
SIFT
and
SURF
respectively are conducted for spherical matching. Each
SIFT
and
SURF
implementation is run with the same parameter
configuration. The setup proposed in Lowe (2004) is applied
to
SIFT
-based methods while thresholds for the Fast-Hessian
detector of
SURF
and the ratio test are set as 1000 and 0.7,
respectively. Referring to Taira
et al
. (2015), the correctness
of the matches is judged using the condition
f
(
p
,
p
′
)=
∠
(
p
,
R
–1
p
′
)
where (
p
,
p
′
) indicates a point match and
R
is an
a
priori
known rotation matrix. If
f
(
p
,
p
′
) is smaller than an
angular threshold, the match is deemed correct. The number
of matches derived from two identical unrotated images is
treated as reference, which comprises 8,726 points in this
case. Table 2 presents the repeatability score of each method
whereas Figure 5 shows the trends of each repeatability while
rotating ω.
Although there is no best feature descriptor can tackle all
kinds of deformation at present,
SURF
has shown its robust-
ness and efficiency in the literature (e.g., Juan and Gwun
2009; Hamid
et al
., 2012; Panchal
et al
., 2013). In the light of
Table 2 and Figure5, the
SURF
-based methods show slightly
superiority in repeatability over
SIFT
-based methods, but
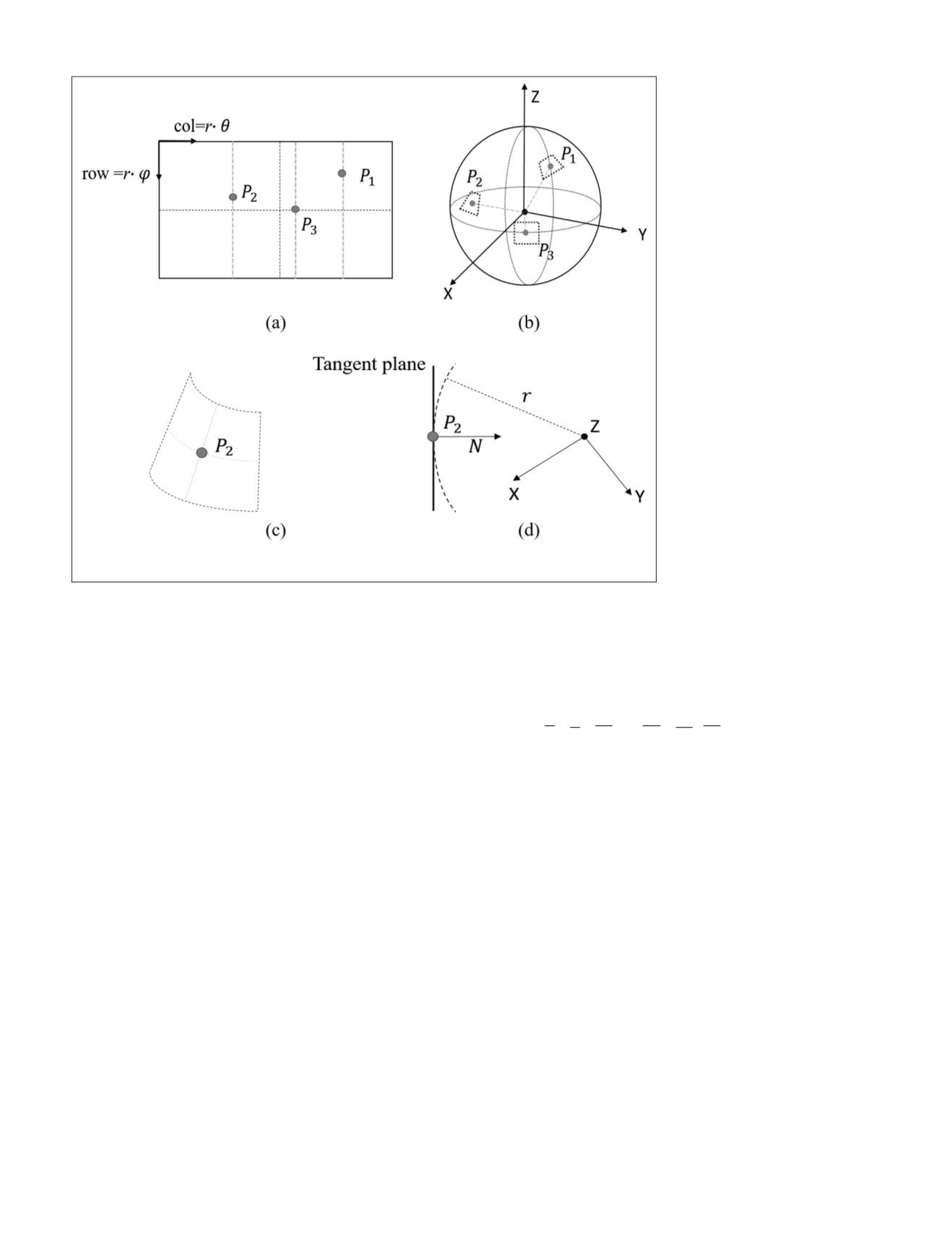
Figure 3. Tangent plane mapping at
P
2
where (a) Detected feature points; (b) Features
on its sphere; (c) Pixels in the cropped region of
P
2
; and (d) Tangent plane crosses
P
2
.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
January 2018
27


