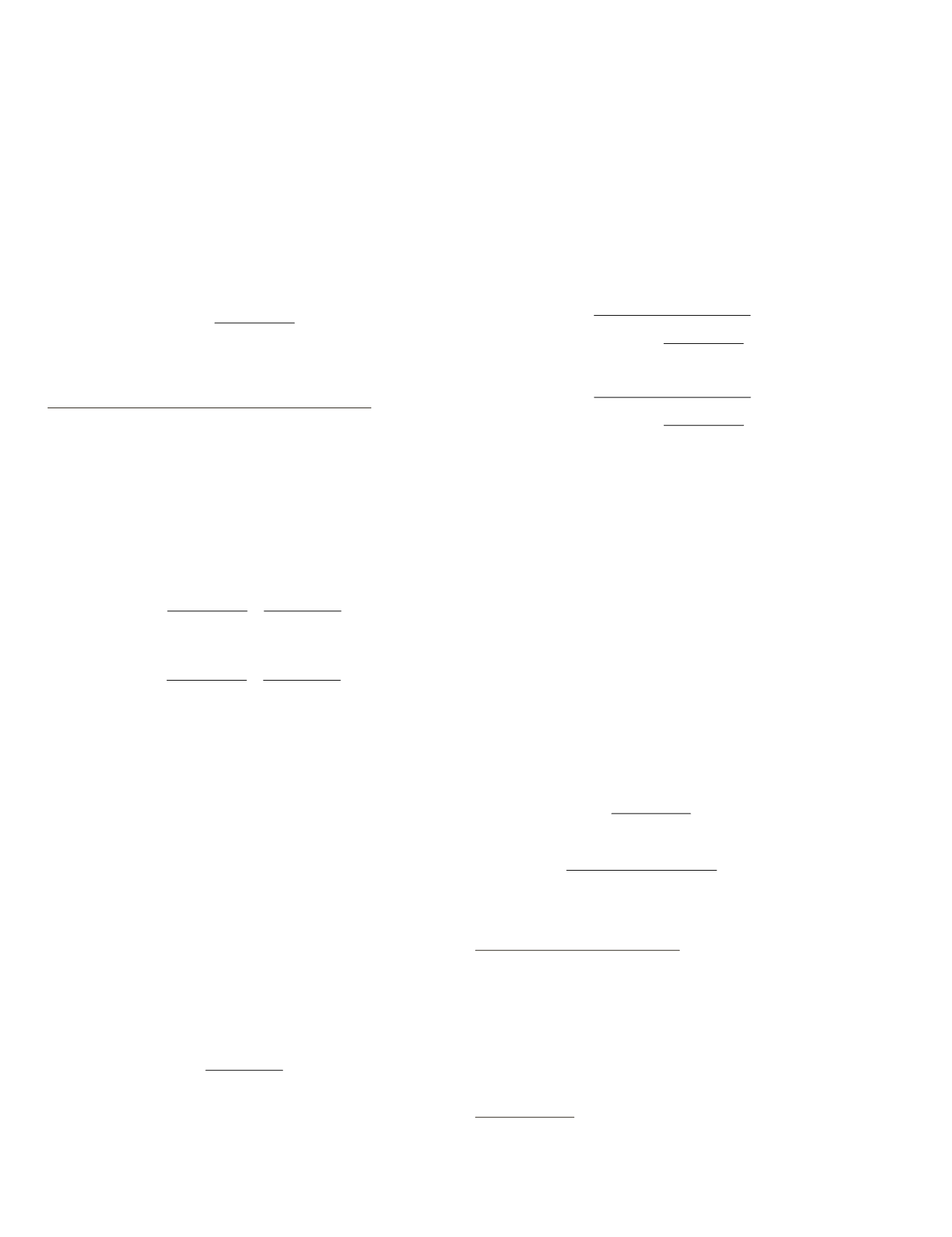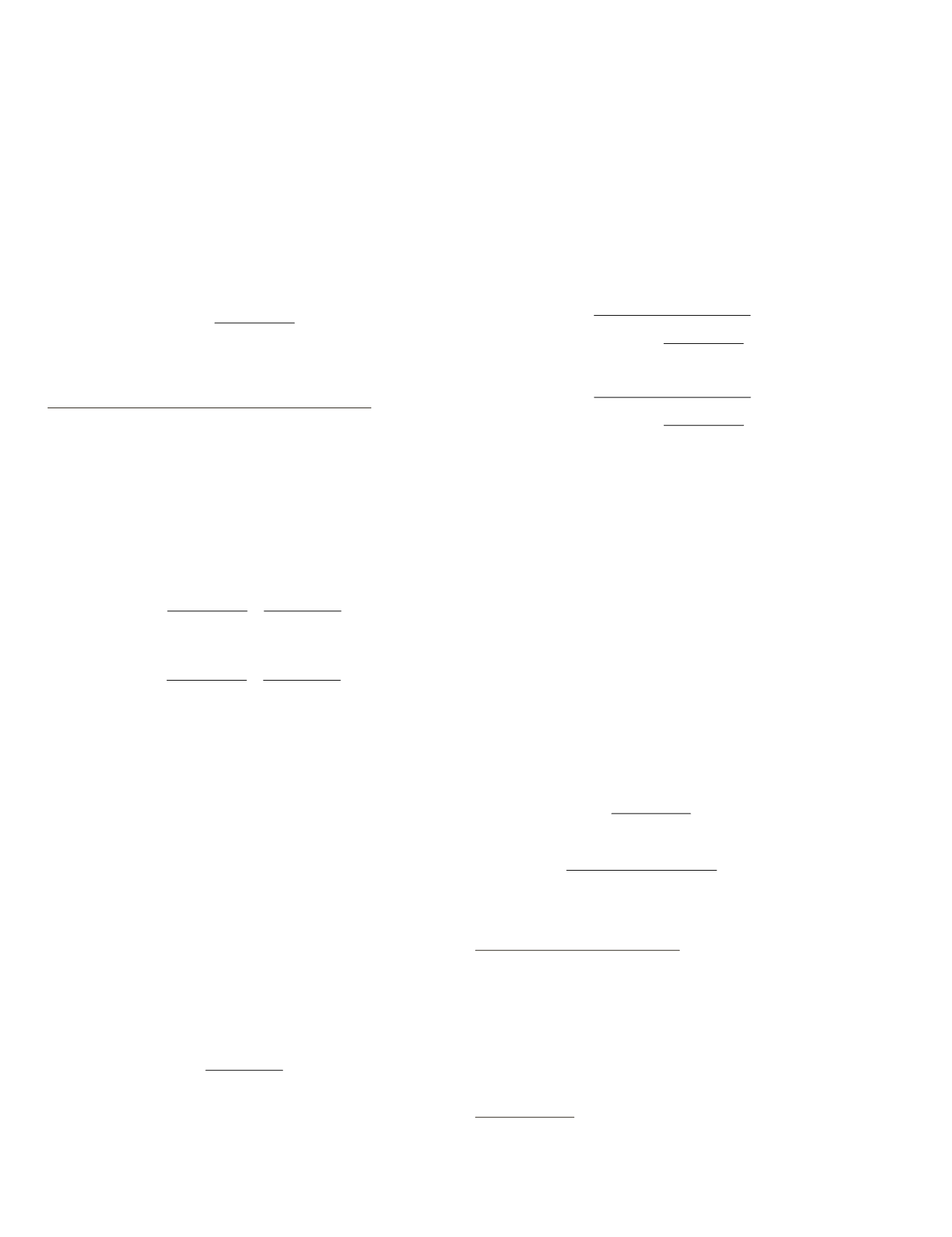
The range of
RA
sub
ij
and
RA
super
ij
is also [0,1]. As the value of
the index approaches 1, the segmentation is more ideal.
Weidner (2008) defined the Quality Rate
(
QR
)
index. When
the area of overlap between the reference object and the cor-
responding object is equal to their union region, the reference
object and the corresponding object completely coincide. In
this situation, the area similarity of the reference object and
the corresponding object reaches a maximum, which indi-
cates an ideal segmentation result. Compared to
FCSP
and
AFI
,
QR
considers not only the overlap region between the
reference object and the corresponding object, but also the
similarity of the two objects. Thus,
QR
is capable of evaluating
geometric relationships more objectively.
QR
area r s
area r s
s S
ij
i
j
i
j
j
i
= −
(
)
(
)
∈
∪
1
1
∩
,
*
(13)
QR
ij
ranges from [0,1], and 0 is the ideal value.
Over-Segmentation Region and Under-Segmentation Region:
Clinton
et al
. (2010) improved on
RA
sub
and
RA
super
, and
proposed the Over-Segmentation
(
OS
)
index and the Under-
Segmentation
(US)
index. Compared to
RA
sub
and
RA
super
, the
two newly proposed indexes replaced the overlapping object
with the corresponding object, while replacing the overlap
region with over-segmentation region or under-segmentation
region. The indexes evaluate the degree of over-segmentation
and under-segmentation by measuring the area ratio of over-
segmentation region to the reference object and the area ratio
of under-segmentation to corresponding object.
OS
area r s
area r
area r s
area r
s S
ij
i
j
i
i
j
i
j
i
= −
(
)
( )
=
−
(
)
( )
∈
1
1
∩
,
*
(14)
US
area r s
area s
area s r
area s
s S
ij
i
j
j
j
i
j
j
i
= −
(
)
( )
=
−
(
)
( )
∈
1
1
∩
,
*
(15)
OS
is usually combined with
US
into the
ED1
index as a
composite evaluation index. Both indexes have the range of
[0,1]. Zero indicates that neither over-segmentation phenom-
enon nor under-segmentation phenomenon exist.
Ideally there should not exist any over-segmentation
phenomenon and under-segmentation phenomenon in the
segmentation results. If the classifier was designed reason-
ably and all of the corresponding objects were classified into
the same class as the reference objects, the over-segmentation
region can still be classified correctly and will not affect
the final classification result. However, under-segmentation
phenomena will inevitably affect the accuracy of the classi-
fication result, due to the misclassification of the under-seg-
mentation region (Marpu
et al
., 2010; Weidner, 2008). Based
on this, Liu
et al
. (2012) improved the US index and proposed
the Potential Segmentation Error
(
PSE
)
index.
PSE
indirectly
enables the evaluation of the segmentation result by calculat-
ing the ratio of misclassification, which is the area ratio of the
under-segmentation region to the reference object.
PSE
area s r
area r
s S
j
i
i
j
i
=
−
(
)
( )
∈
,
*
1
(16)
PSE
’s value ranges from 0 to plus infinity, and the 0 value
indicates that there is no under-segmentation phenomenon in
the reference objects.
As a composite index, the
ED2
index is a combination of
PSE
and Number of Segments Ratio
(
NSR
)
.
ED2
is the most reli-
able when
PSE
and
NSR
have the same order of magnitude.
ED2
considers both the geometric discrepancies and the arithmetic
discrepancies in the segmentation result. However, when the
reference objects are segmented into a massive number of
segmented objects, it is hard to align the order of magnitude
between
NSR
and
PSE
. In addition, the coexistence of one-to-
many over-segmentation and many-to-one under-segmenta-
tion may result in an invalid
NSR
index. To address this issue,
Yang
et al
. (2014) improved
NSR
,
PSE
, and
ED2
and proposed
the Over-Segmentation 2
(
OS2
)
index and Under-Segmentation
2
(
US2
)
index based on the average value of local under-seg-
mentation ratio and local over-segmentation ratio.
OS
area r s
area r
s S
i
j
i
j
i
j
i
2
1
1
=
−
(
)
∈
∑∑
∩
( )
,
*
(17)
US
area r s
area s
s S
i
j
i
j
j
j
i
2
1
1
=
−
(
)
∈
∑∑
∩
( )
,
*
(18)
OS2
and
US2
are normalized indexes, and their value are
both in the range of [0,1]. They are often integrated into
ED3
to evaluate global geometric discrepancies, as well as arithme-
tic discrepancies.
Cheng
et al
. (2014) put forward the Omission Error
Index
(
OE
)
and the Commission Error Index
(CE)
based on
the object-fate matching method.
OE
is the area ratio of the
overlap region between the Invading objects and the refer-
ence object, in the over-segmentation region, to the reference
object.
CE
refers to the area ratio of the remaining regions
except the overlapped regions between the Expanding objects
and the reference object, in the under-segmentation region, to
the reference object. From the point of view of the calculation
principle,
OE
is equivalent to
OS
, and
CE
is equivalent to
PSE
.
Therefore,
OE
and
CE
are over-segmentation and under-seg-
mentation indexes, respectively, exclusive of the object-fate
matching method and can be used as a composite index when
combined with object-fate, based on the arithmetic discrep-
ancy index.
OE
area r s
area r
s Invading
i
i
l
i
l
i
=
(
)
∈
∩
( )
,
(19)
CE
area s area r s
area r
s Expanding
i
k
i
k
i
k
i
=
( )
−
(
)
∈
∩
( )
,
(20)
The ideal value of
OE
i
and
CE
i
is 0.
Location and Boundary-Based Indexes
Indexes based on location and boundary measure the geo-
graphic discrepancy between the reference object and the cor-
responding object as well. However, unlike the indexes based
on area, which evaluate the segmentation result by measuring
the degree of coincidence, over-segmentation, and under-
segmentation, these indexes based on location and boundary
evaluate the segmentation result by measuring the position
similarity and the contact ratio of the boundary between the
reference object and the corresponding object.
Based on Location
Zhan et al. (2005) proposed the Quality of Object Location
index
(qLoc)
to evaluate the location similarity between the
634
October 2018
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING