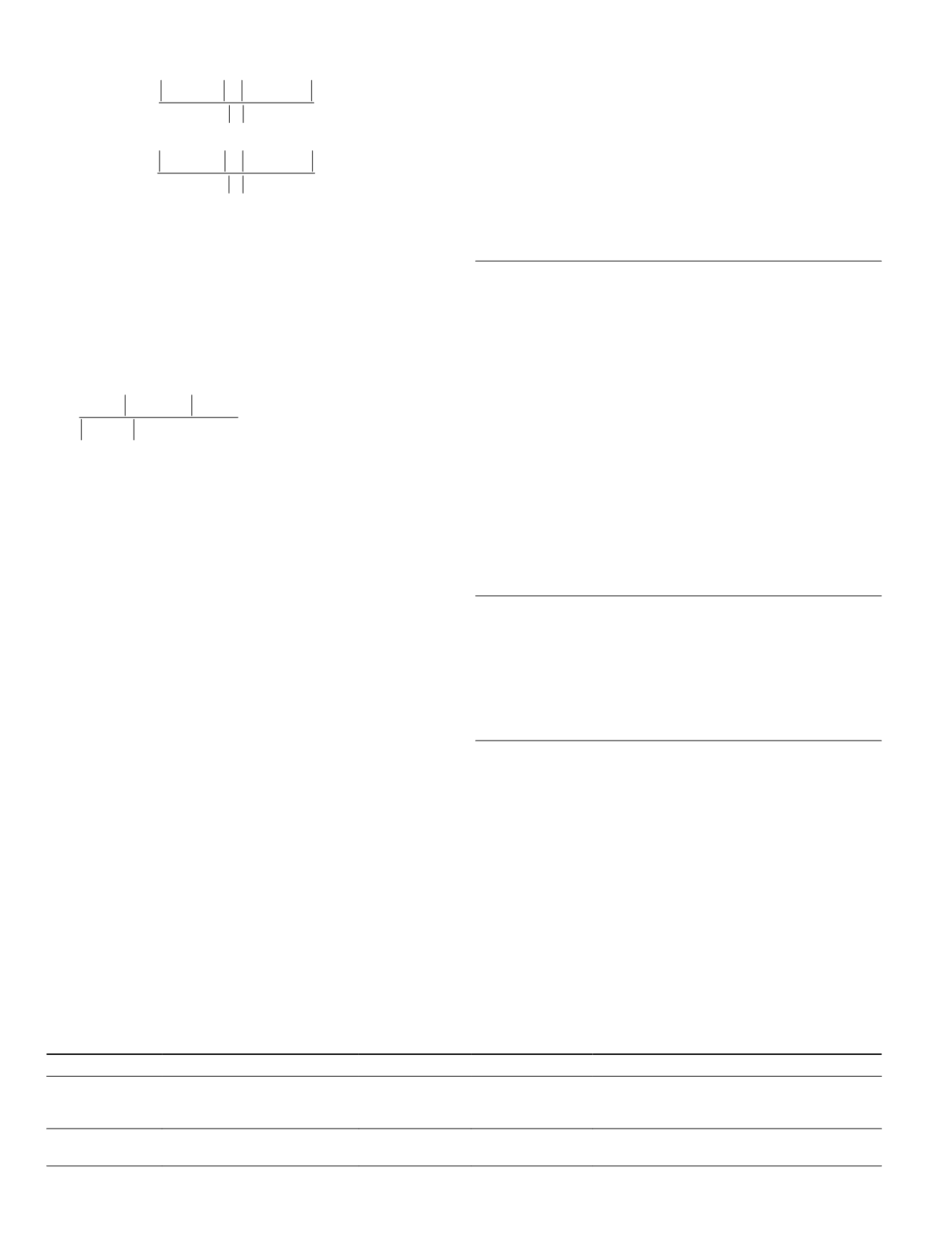
Pos Q L Zero Q L
Q
T
,
,
( )
+
( )
≥
1
(8-1)
or ,
Neg Q L Zero Q L
Q
T
,
,
( )
+
( )
≥
1
(8-2)
where
T
1
is close to 1.0. Segment
Q
is then positively tan-
gent to
L
(8-1) or negatively tangent to
L
(8-2).
Segmentation and line extraction errors also cause se-
mantically meaningless unilateral and tangent relationships
between segments and straight lines. To use only meaningful
unilateral and tangent relationships for segmentation, the
length of
L
must be large, and the length of
Proj
(
L,Q
)
should
not exceed too much that of the parts of
L
that fall in and
touch segment
Q
.
½
L
½
≥
T
2
,
(9-1)
and
Proj L Q
In L Q Touch L Q
T
,
,
| ( , )|
( )
( )
+
≤
3
(9-2)
If segments
Q
and
R
both satisfy Equation 8 and are located
on the same side of
L
, then these segments are labeled as pos-
sible
IPSL
-neighbors with respect to line
L
. If segments
Q
and
R
both satisfy Equation 9, then they are considered
IPSL
-neigh-
bors, that is, an
IPSL
-neighborhood relationship exists between
Q
and
R
(with respect to
L
)
.
Equation 9 prevents straight line
L
from being semantically meaningless (the length of line
L
is too small; Equation 9-1) or possibly being “born by” other
objects (the part of
L
owned by
Q
is too small compared with
the size of
Q
; Equation 9-2). Multiple
IPSL
-neighborhood rela-
tionships between segments
Q
and
R
with respect to multiple
co-related straight lines could possibly exist. Figure 2 shows
typical positive and negative cases of segment–line models.
Straight-line Constrained Merging
We employ the same merging cost criterion proposed by Baatz
and Shäpe (2000). This merging cost criterion that measures
visual similarities among segments has been implemented
in eCognition and used in our previous work (Wang and Li,
2014). However, these similarity measures cannot guarantee
that merging fully coincides with the naked eye. In this study,
a straight-line constraint is adopted to strengthen these simi-
larity measures. A straight-line-based merging step is applied
to the original method to embed straight-line information into
the segmentation. That is, a remerging step guided by
IPSL
-
neighborhood is implemented on the OPs obtained from the
non-constrained merging of
HBC-SEG
. This step requires a new
merging cost threshold called straight-line scale (
T_SL
). Its
minimal-merging-cost neighbor and
IPSL
-neighbors are first
obtained in consideration of a segment waiting for possible
merging. If the minimal-merging-cost neighbor equals one
member in the
IPSL
-neighbors and the merging cost is less
than the power of
T_SL
, the segment can be merged with this
neighbor. This empirical setting (power of
T_SL
), which accel-
erates the merging processes to produce suitable ground object
sizes, is similar to that in literature (Baatz and Shäpe, 2000).
All segments that do not satisfy the above conditions
cannot be merged. The core idea is the re-merging of
IPSL
-
neighbors with a loose merging threshold instead of a unique
global remerging threshold for all segments. This merging
scheme effectively reduces over-segmentation and prevents
under-segmentation errors caused by unreasonable merging.
When no
IPSL
-neighbors exist in the image, straight-line con-
strained merging does not take effect, and the refined method
degenerates to the original version. The detailed pseudo-code
is presented below.
M
erging
algorithm
constrained
by
IPSL
-
neighborhood
Inputs: segment set {
p
0
}, straight line merging threshold
T_SL
;
Outputs: primitive set {
p
};
Begin: obtain the minimal-merging-cost neighbor and
IPSL
-neigh-
bors for all segments in {
p
0
};
For each segment
m
in {
p
0
}{
Obtain its minimal-merging-cost neighbor
n
and
IPSL
-neighbor set
{
q
};
If
n
equals one of {
q
}, set the merging cost threshold (
Th_m
) of
m
to
the power of
T_SL
; otherwise, set
Th_m
to a large negative value;
If merging cost
t
between
m
and
n
is larger than
Th_m,
Output
m
directly into the new segment set {
p
1
}; //no merging oc-
curs
Else { //merging occurs
If segment
n
has been merged before, e.g.,
into segment
o in
{
p
1
};
Merge
m
into
o
;
Else
Merge
m
and
n
into a new segment in {
p
1
};
}
}
If segment merging still occurs {
Rebuild topology relationship for {
p
1
};
Replace {
p
0
} by {
p
1
};
Go to Begin;
}
Else output {
p
1
}as {
p
};
Experiments
The algorithm was implemented with Visual C++ 2010, and
the operating system used was Windows-7 with an Intel(R)
Xeon(R) E5620 2.40
GHz
CPU
and 3.48
GB
RAM
. The refined and
original methods were applied on different
HSR
images for
method validation and comparisons.
Experimental Data
The proposed algorithm was applied and compared in several
HSR
images with different imaging types, resolutions, and
band numbers. We selected two representative areas for
method demonstration. Table 1 shows the image type, resolu-
tion, size, imaging date, and location of these testing areas.
Experimental Procedure
In our previous work (Wang and Li, 2014), we analyzed and
verified the numerous advantages of
HBC-SEG
over
FNEA
in
T
able
1. E
xperimental
D
ata
Experimental area
Image type
Image resolution Image size (pixels)
Data description
Area 1
True-color aerial image with
three bands
0.3 m
905 × 664
Downloaded from Ohio Statewide Imagery
Program (OSIP,
)
and collected from February to March 2007
Area 2
ALOS panchromatic image
with one band
2.5 m
385 × 231
Collected in February 2007 and located in
Jiangning, Nanjing, China
400
May 2015
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING


