PE&RS May 2015 - page 398

Many studies on FNEA improvement have been conducted.
Typical schemes include applying automatic approaches to
best-scale selection (Drǎguţ et al., 2010 and 2014; Tullis et al.,
2010; Tong et al., 2012) or using several auxiliary data sources,
e.g., GIS database, digital map, or lidar data (Smith et al., 2010;
Anders et al., 2011). Different segmentation methods, e.g.,
combining edge and region information, have also been sug-
gested. For example, Kermad and Chehdi (2002) proposed the
over-segmentation of images on the basis of both edge detection
and region merging ,and then iteratively refining the segmenta-
tions with gradually relaxed constraints until both methods
achieve dependable, coherent results. Li et al. (2010) extracted
image edges by using an edge detector embedded with con-
fidence and then used the edges in marker-based watershed
segmentation. Remote sensing image segmentation showed
that their method improves boundary positional precision and
reduces over-segmentation. Chen et al. (2012) proposed an
edge-constrained multi-resolution segmentation method. The
merging of segments was controlled by both scale parameter
and edge intensity. Edge intensity was weighted by spectral
distances among “adjacent partitioned regions.” Yu et al.
(2012) proposed a segmentation and classification algorithm for
synthetic-aperture radar (SAR) imagery. Their method incorpo-
rates region growing and a Markov random field edge strength
model. In our previous study (Wang and Li, 2014), we pro-
posed HBC-SEG , which considers the issues of over- and under-
segmentation and scale-parameter dependency, and showed
the advantages of HBC-SEG over FNEA in the above aspects.
Although over-segmentation error is less serious than
under-segmentation error, such error still influences the
subsequent information extraction steps of OBIA . For example,
over-segmentation can result in imprecise feature extraction
for shapes and textures within and topology relationship
among OPs. Thus, over-segmentation requires careful consid-
eration and should be avoided. In HBC-SEG and FNEA, the scale
parameter can be increased to re-merge these segments and
consequently reduce over-segmentation errors. However, the
risk of under-segmentation errors is unavoidable given the
global increase in segments. Thus, robust schemes need to be
designed and utilized.
In HBC-SEG, image edges are used as the constraint to guide
segment merging; thus, this method exhibits good segmenta-
tion accuracy. However, the trivial inner details of ground
objects may influence edge extraction and produce redun-
dant or “false” edges, which cause fragmented segments,
i.e., over-segmentation errors. To overcome this drawback,
straight-line information is added to this method. In edge
extraction, man-made objects with straight boundaries can
be located and extracted through straight edge line detection.
In image segmentation, segments located along the same side
of a common straight line are assumed to be highly related
or belong to the same object. Such segments are possibly
over-segmented and should be merged. Straight edge lines
are utilized to refine HBC-SEG to obtain accurate segmentation.
Compared with HBC-SEG and FNEA, the straight-line constraint
in the refined method helps reduce the trivial inner details
of segments typically within man-made objects and further
reduces over-segmentation errors.
Methodology
Prior to the discussion of the technical framework and routes,
the following hypotheses are first established to clarify our
ideology.
Hypothesis 1: If spatial objects are located closely and visu-
ally similar, they are assumed to be semantically homoge-
neous, i.e., belonging to one semantic category.
Hypothesis 2: Under Hypothesis 1, if spatial objects are
further arranged into a semantically meaningful configura-
tion, e.g., a straight line, they are believed to be semanti-
cally homogeneous.
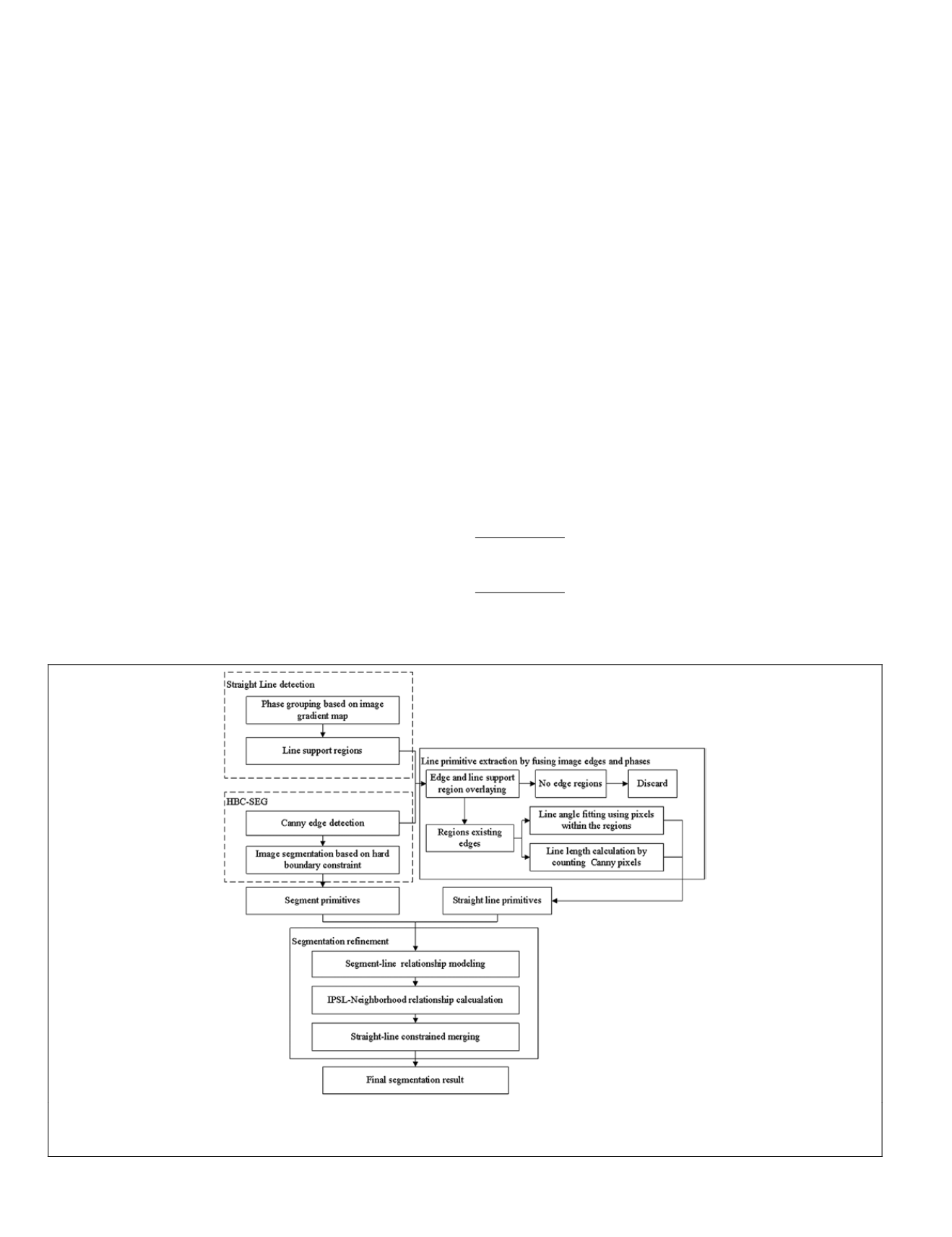
Figure 1. Technical framework. HBC-SEG is first implemented to obtain the segment primitives; Burns’ phase grouping method is used
to obtain the straight line primitives. After building the relationships between the two types of primitives, a refinement step is applied to
HBC-SEG to re-merge the segments and obtain the final results.
398 May 2015 PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING