Hypothesis 3:
If the neighboring segments obtained through
image segmentation are visually similar and arranged
along the same side of a straight line, they are assumed to
be over-segmented and should be merged into one segment.
Hypothesis 1 is intuitive. Hypothesis 2 is an enhanced
version of Hypothesis 1 given that it involves more spatial
constraints, which reduce misjudgments in spatial reasoning.
Hypothesis 3 is a specific version of Hypothesis 2 for image
segmentation. In this scenario, neighborhood relationship
guarantees that segments are close; a straight line represents
a “semantically meaningful” configuration, and “belonging to
one segment” indicates semantic homogeneity. In accordance
with Hypothesis 3, a segment-line relationship model is cre-
ated and further extended into a refined segmentation method
to reduce over-segmentation errors.
The technical framework of the refined method is presented
in Figure 1. First, OPs are obtained from
HBC-SEG
, which also
produces gradient and Canny edge maps (Canny, 1986). The
gradient map is regrouped into line support regions through
Burn’s phase grouping method (Burn
et al
., 1986), and straight
lines are detected. Second, line support regions are overlaid
with Canny edges for edge-phase-combined straight-line primi-
tive extraction. Third, segment-line topology is calculated. The
IPSL
-neighborhood relationships among OPs are obtained in the
segment-line topology and utilized for straight-line constrained
merging (refinement step) until the merging cost exceeds the
threshold; then, the entire segmentation process ends.
HBC-SEG Method
This method involves a two-stage merging process. In the
first stage, a multi-spectral Canny edge detection method is
employed to extract remote sensing image edges. The edges
are then embedded into watershed segmentation (Vincent and
Soille, 1991) for initial-segment segmentation. The initial sub-
OPs, i.e., the bases of subsequent merging, are obtained after
edge allocation. Next, edge-constrained merging is adopted
to iteratively combine these sub-OPs until all merging costs
exceed a maximized threshold, thus creating the initial OPs.
Non-constrained merging under the control of a significantly
small threshold converts the initial OPs into final OPs. The
first-stage merging allows for the growth of the segments but
is limited by the image edges. In the second stage, trivial
segments are removed by being merged into one another or
into large segments.
HBC-SEG
exhibits good segmentation ac-
curacy, including over- and under-segmentation accuracy. The
OP
boundary obtained with this method is highly consistent
with the actual boundaries (edges) of ground objects. This
method facilitates the utilization of edges and straight lines in
segment-line relationship modeling.
Straight-line Primitive Extraction
On the basis of the gradient map obtained from
HBC-SEG
,
straight lines are detected through phase grouping method
(Burn
et al
., 1986). This method is fast and concise in prin-
ciple. However, this method tends to be influenced by image
noise and extracts miscellaneous lines. Thus, a concise edge-
phase-combined straight-line detection method is designed.
Line support regions are overlaid with Canny edges, and
regions without fallen edges are discarded. Straight lines are
extracted for the remaining regions, and line features, in-
cluding lengths and directions, are calculated. Such straight
lines (which are called straight-line primitives) are used in
segment-line modeling.
Segment-line Relationship Modeling
We let
Q
and
R
be two sub pixel sets within image
I
.
Q
= {
q
i
= (
x
i
,
y
i
)
½
∈
[1,
k
],
k
=
½
Q
½
} and
R
= {
r
i
= (
x
i
,
y
i
)
½
∈
[1,
k
],
k
=
½
R
½
} ,
where
x
and
y
are the pixel coordinates and
½×½
is the potential
of a set.
Q
and
R
fit the definition of segments obtained by im-
age segmentation (Gonzalez and Woods, 1992). We let straight
line segment
L
be a pixel set in
I
:
L
= {
l
i
= (
x
i
,
y
i
)
½
∈
[1,
k
],
k
=
½
L
½
};
L
fits the following straight line equation:
Z
L
=
y
–
ax
–
b
= 0,
(1)
where
a
and
b
are the coefficients. To establish the adaptable
segment-line relationships, segments
Q
and
R
need to inter-
sect line
L
as follows:
Q
Ç
L
≠
Ø,
R
Ç
L
≠
Ø
(2)
Two spatial operator sets, namely, direction and topology
operator sets, are defined. These sets work on segments and
straight lines and produce their subsets. The direction opera-
tor set is defined as follows:
Dir
(
Q,L
)={
Neg
(
Q,L
),
Zero
(
Q,L
),
Pos
(
Q,L
)},
(3)
which denotes a subset extracted from
Q
that is located above,
on, or below line
L
. For example, operator
Neg
(
Q,L
) is defined
as follows:
Neg
(
Q,L
) = {
q
i
= (
x
i
,
y
i
)
½
y
i
–
ax
i
–
b
< 0}
(4)
The other two are in similar forms. We let
B
Q
be the bound-
ary pixels of
Q
defined by four connected neighborhoods. The
topology operator set is defined as:
Top
(
L,Q
) = {
In
(
L,Q
),
Touch
(
L,Q
),
Out
(
L,Q
),
Proj
(
L,Q
)}. (5)
The first three operators denote a subset extracted from
L
,
which is contained by, touched by, or located outside
Q
. For
example, operator
Touch
(
L,Q
) is defined as
Touch
(
L,Q
) = {
l
i
½
l
i
∈
B
q
,
l
i
∈
L
}.
(6)
Operator
Proj
(
L,Q
) denotes the straight line segment ob-
tained by vertically projecting
Q
onto
L
(Figure 2c).
Segment
Q
is considered unilateral and tangent to line
L
if
Equation 7 is satisfied.
½
Pos
(
Q,L
)
½
+
½
Zero
(
Q,L
)
½
=
½
Q
½
or
½
Neg
(
Q,L
)
½
+
½
Zero
(
Q,L
)
½
=
½
Q
½
(7)
The above conditions are relaxed given the possible errors
in image segmentation and straight line extraction.
Q
is uni-
lateral and tangent to
L
as long as Equation 8 is satisfied.
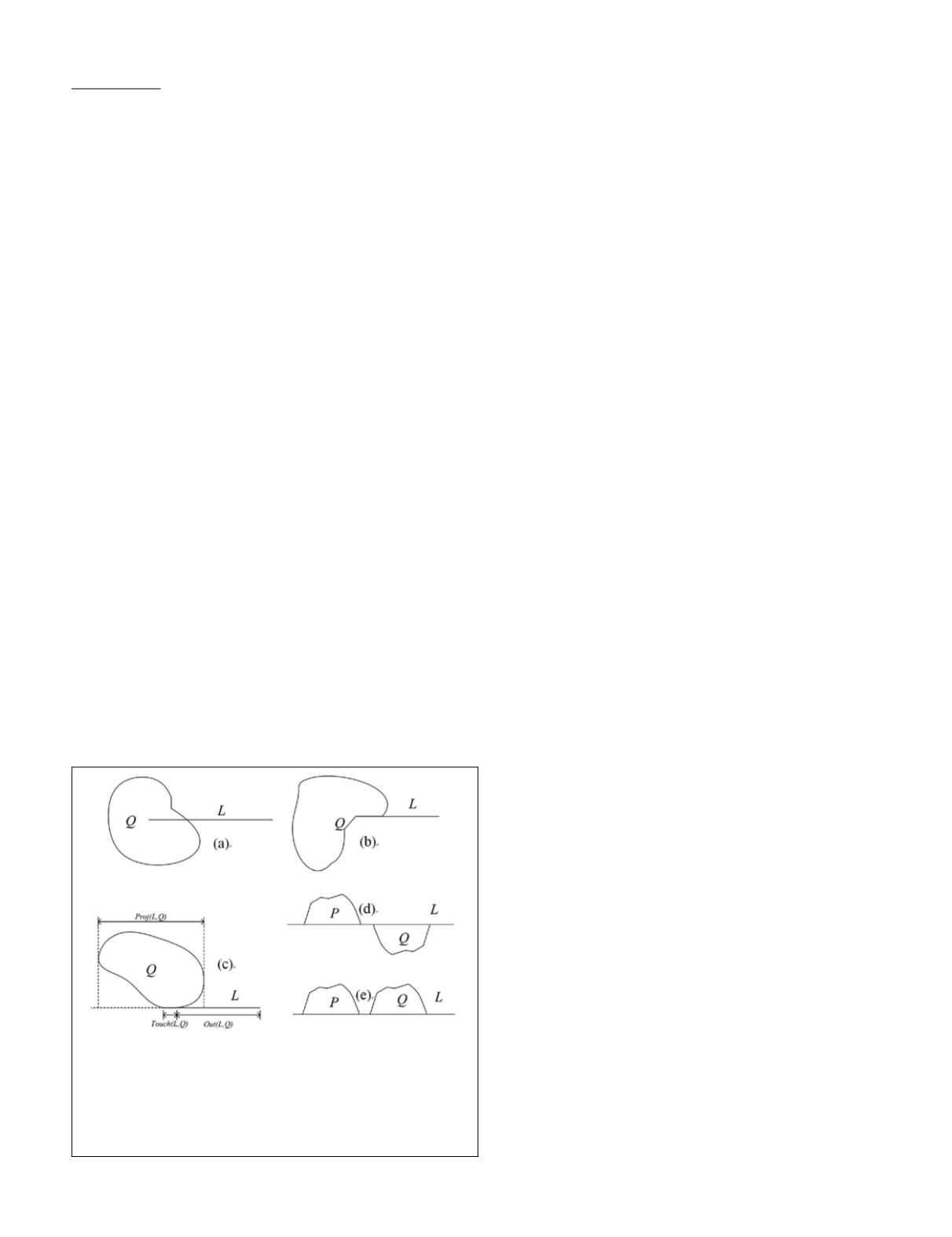
Figure 2. Segment-line modeling. In Figures 2a and 2b, segment
Q
is located bilaterally to line
L
. In Figure 2b, segment
Q
is tangent
but not unilateral to line
L
. In Figure 2c, segment
Q
is unilateral
and tangent to line
L
but does not satisfy Equation 9-2. In Figure
2d, segments
P
and
Q
are located bilaterally to line
L.
Only
P
and
Q
in Figure 2e fully satisfy all model requirements and can be
called IPSL-neighbors.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
May 2015
399


