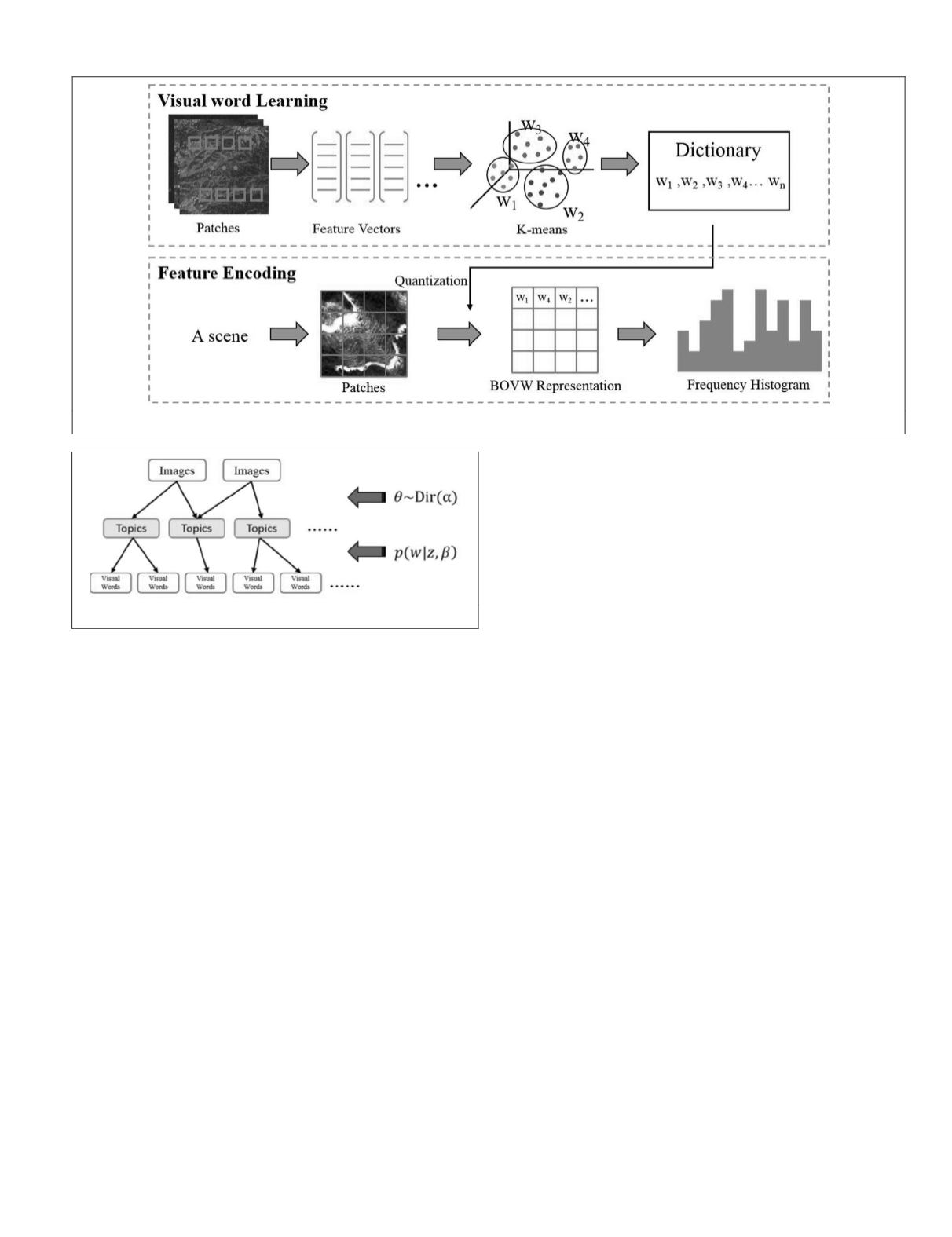
1. For the scene d, a
K
-dimensional topic proportion
θ
is
chosen according to a Dirichlet distribution Dir(
α
), where
K
is the number of topics.
2. For each visual word position in the scene, a topic
z
is
first chosen from the multinomial distribution Mul(
θ
), and
then a visual word
w
is chosen from
p
(
w
|
z
,
β
), a multino-
mial probability conditioned on topic
z
.
The above process shows that the model is controlled by
α
and
β
, and thus in the learning stage, our goal is to find the
two parameters such that the log likelihood of the image
dataset is maximized. It is clear that
LDA
is an unsupervised
model, and the estimated topics are not specifically for classi-
fication. To mark the category of a document directly, Jon and
David (2008) developed
sLDA
, which is a supervised variant
of
LDA
, and proved that
sLDA
fitted the category of documents
better than
LDA
. Since we are more concerned about the cat-
egory than the topics of the scene, the
sLDA
model is applied
to tea garden scene detection in the proposed framework.
As described in Jon and David (2008),
sLDA
adds a response
variable which denotes the categories of the scenes (i.e., tea
gardens and non-tea gardens in our study) in the generative
process of
LDA
. After generating a scene, the response variable
associated with this scene is also generated. Thus, the learned
model can then be used to classify the unknown scenes.
Unsupervised Feature Learning
In the proposed framework, the
UCNN
, via the plain
k
-means
clustering method, is constructed to achieve unsupervised
multi-layer feature learning (Li
et al.
, 2016). As depicted in
Figure 4, the
UCNN
is composed of two feature extraction lay-
ers, and each layer contains three operations: convolution,
local pooling, and global pooling. In the following, we take
the first feature extraction layer as an example to introduce
the three operations.
1. Convolution operation: The function of the convolution
operation is feature mapping, which is defined under the
constraint of function bases. The function bases need to
be generated by an unsupervised learning algorithm, and
k
-means clustering is utilized in the proposed frame-
work due to its good performance (Coates et al., 2010).
As described in Li et al. (2016), the unlabeled patches
with dimension
w
–
w
–
d
are randomly sampled from
the original image scenes, where
w
denotes the size of the
receptive field, and
d
is the number of image channels. We
can then construct the feature set X = {
x
1
,
x
2
, …,
x
M
}, where
x
i
∈
R
N
(
N
=
w
*
w
*
d
) denotes the vectorization vector of the
i – th
patch. After preprocessing by intensity normaliza-
tion and zero component analysis whitening, the feature
set
X
is clustered by the
k
-means clustering approach, and
the clustering centers form the function bases C = {
c
1
,
c
2
,
…,
c
K
}, with
c
i
∈
R
K
. Once the function bases are generated,
the convolution operation can be defined as follows. Let
p
denote the vectorization vector of one sliding patch in
the input image I, then this patch can be mapped onto the
sparse feature vector
f
∈
R
K
:
f
k
= max{0,
μ
(
z
) –
z
k
}
(1)
where
z
k
= |
p
–
c
K
|
2
,
k
= 1, 2, …,
K
and
μ
(
z
) is the mean
of the elements of
z
. Through the convolution operation,
we produce the feature map F of the input image I with
dimension (
h
–
n
) – (
h
–
n
) –
d
, where
h
denotes the size
of image I.
2. Local pooling operation: This pooling operation is imple-
mented to keep slight translation and rotation invariance.
Here, the local pooling operation is defined as:
a. L(
i
/
s
,
j
/
s
,
k
) = max(F(
i
–
s
/2:
i
+
s
/2:
j
–
s
/2:
j
+
s
/2:)) (2)
where
k
= 1, 2, …,
K
and
s
denotes the local window size
of the pooling operation,
3. Global pooling operation: The aim of the global pooling
operation is to reduce the dimension of the feature. In the
implementation, the output of the local pooling operation
Figure 2. Flowchart of the
BOVW
model.
Figure 3. Generative process of
LDA
.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
November 2018
725


