October 2019 Layout Flipping Full - page 755

independent records for the laser-unit data and raw naviga-
tion data (GNSS receivers and microelectromechanical IMU).
The Ibeo LUX 2010 and navigation-system devices were
arranged in a payload carried by UAV octocopter (Sensormap
Sx8, Figure 1b). The laser unit was positioned below the
structure. The other devices—including the NovAtel SPAN-
IGM-S1, FlexPak6 receiver, Raspberry Pi microcomputers, con-
nection cables, and battery—were placed inside of the alumi-
num container (Figure 1a). A single-frequency GNSS receiver
(NavSpark NS-RAW) and the GNSS antennae were arranged at a
1-m bar (Figure 1b). After physical device integration, the sys-
tem mounting parameters can be obtained by direct laboratory
measurement and a calibration process, which is described
later under Calibration of the ALS .
Postprocessing Synchronization
A technique to perform off-line time synchronization that
compares signals generated by decoupled devices from an
ALS acquisition for low platform speed (<5 m/s) is presented
in this section. Off-line synchronization can be defined as a
technique that enables the association between sensor posi-
tion estimated by GNSS (GPS time and GNSS height) and lidar
data (laser local time and distance) in a postprocessing step to
estimate the clock differences of these devices and, from these
differences, assign the GPS time to the corresponding lidar
data. The proposed technique requires the following steps: (1)
UAV maneuvers at the beginning and ending of the flight (see
Flight Maneuvers and Data Acquisition); (2) computation of
the clock differences and off-line synchronization by cross-
correlation (see Clock-Difference Estimation and Off-Line
Synchronization); (3) data-synchronization improvements
with LSM (see Refinement by the Least-Squares Method); and
(4) estimation of boresight misalignment of the laser unit
with respect to the IMU (see Calibration of the ALS). The main
contributions of the new synchronization approach presented
in this article rely on the processes described under Clock-
Difference Estimation and Off-Line Synchronization and
Refinement by the Least-Squares Method. The flight maneu-
vers during ALS data acquisition enable flexible ALS data col-
lection with further processing without the need for real-time
synchronization, either in case of failure or when real-time
synchronization is unfeasible or diffic ult.
Flight Maneuvers and Data Acquisition
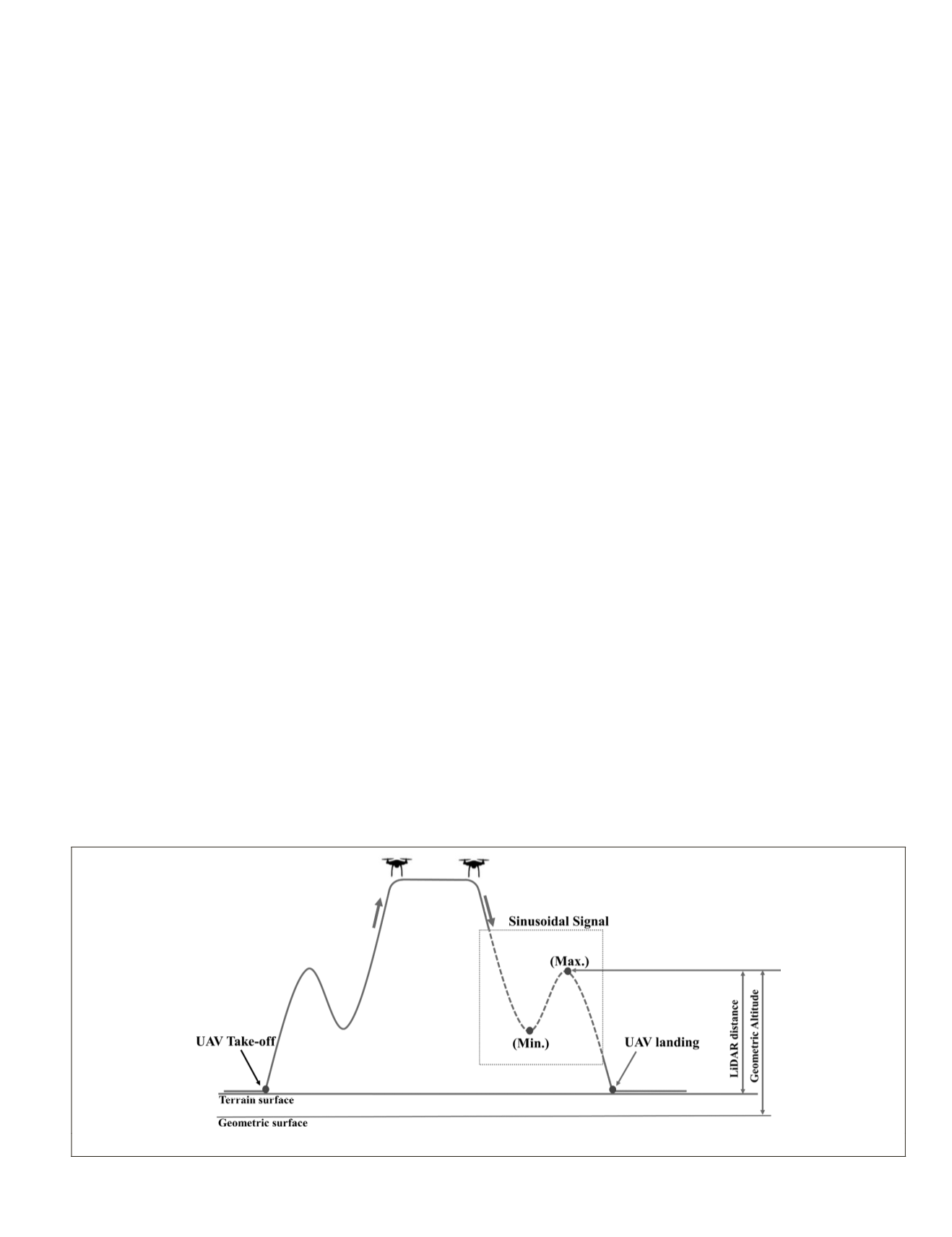
The concept of off-line synchronization proposed is based
on UAV flight maneuvers to generate a signal that enables
comparison between the laser ranges and GNSS altitudes. The
flight maneuvers follow a trajectory with height variations
in a sinusoidal shape just after takeoff and before landing.
Therefore, the laser ranges and GNSS altitude measurements
generate similar signals, as exemplified in Figure 2. A flight
maneuver over flat and non-vegetated terrain is suggested to
ensure a better comparison between laser and GNSS signals.
Significant terrain slope can result in systematic errors in the
synchronization with the proposed technique.
These flight maneuvers generate maximum and minimum
height points in a sequential data acquisition. The matching
between signals (ranges and altitudes) can be performed by
manually or automatically identifying the maximum (Max.)
and minimum (Min.) height points (Figure 2), comparing the
complete sinusoidal signals of the trajectory. This comparison
is used to estimate the clock difference. The automatic option
is investigated and assessed in this article.
Clock-Difference Estimation and Off-Line Synchronization
The proposed method considers that homologous signals (Figure
2) have similar heights (GNSS flight height and lidar range) but
different time reference systems (GPS time and local laser time).
The synchronization process comprises four steps: (1) prelimi-
nary processing, (2) height- and lidar-data resampling, (3) estima-
tion of the clock difference, and (4) correction of the laser time.
1. The lidar data from the Ibeo LUX laser scanner are stored
as sequential packages, which contain information from
four levels of scanning during a data-collection period
(see earlier, under UAV Laser Scanning System). Time
information is present only at the beginning and end of
each packet. Therefore, a time interpolation is necessary to
associate a local laser time with each measurement. After
laser-time interpolation, the data set was clipped to obtain
only the corresponding sinusoidal signals of the trajectory
on the lidar data, which is used as a reference vector to
search the maximum correlation with the GNSS data.
2. Lidar data (distance) and GNSS data (geometric altitude)
were converted to flight heights, which enable comparison
between the sinusoidal signals from the lidar ranges and
GNSS altitude. The flight heights are referenced to the ter-
rain surface (origin), which is comparable to the distance
between the ground and the sensor. The GNSS altitude was
converted from the geodetic coordinate to a flight height
(GNSS height) considering the altitude of the test area
as reference, which was measured by the GNSS receiver
before takeoff (Figure 2). The lidar data were selected ac-
cording to the vertical and horizontal angles to obtain the
shortest distance between the laser unit and the terrain
Figure 2. Maneuvers for data acquisition with the airborne laser scanning devices aboard the unmanned aerial vehicle.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING October 2019 755