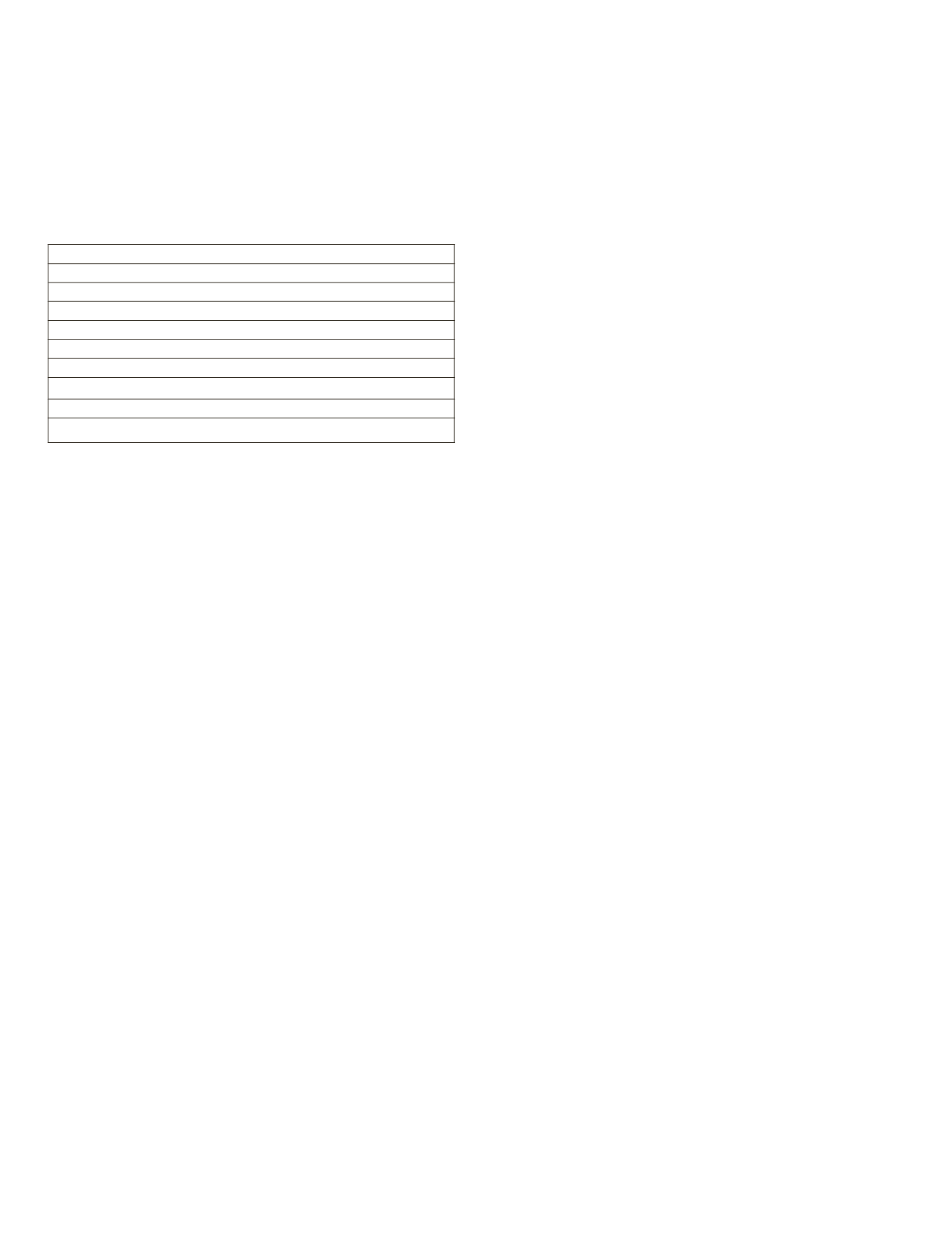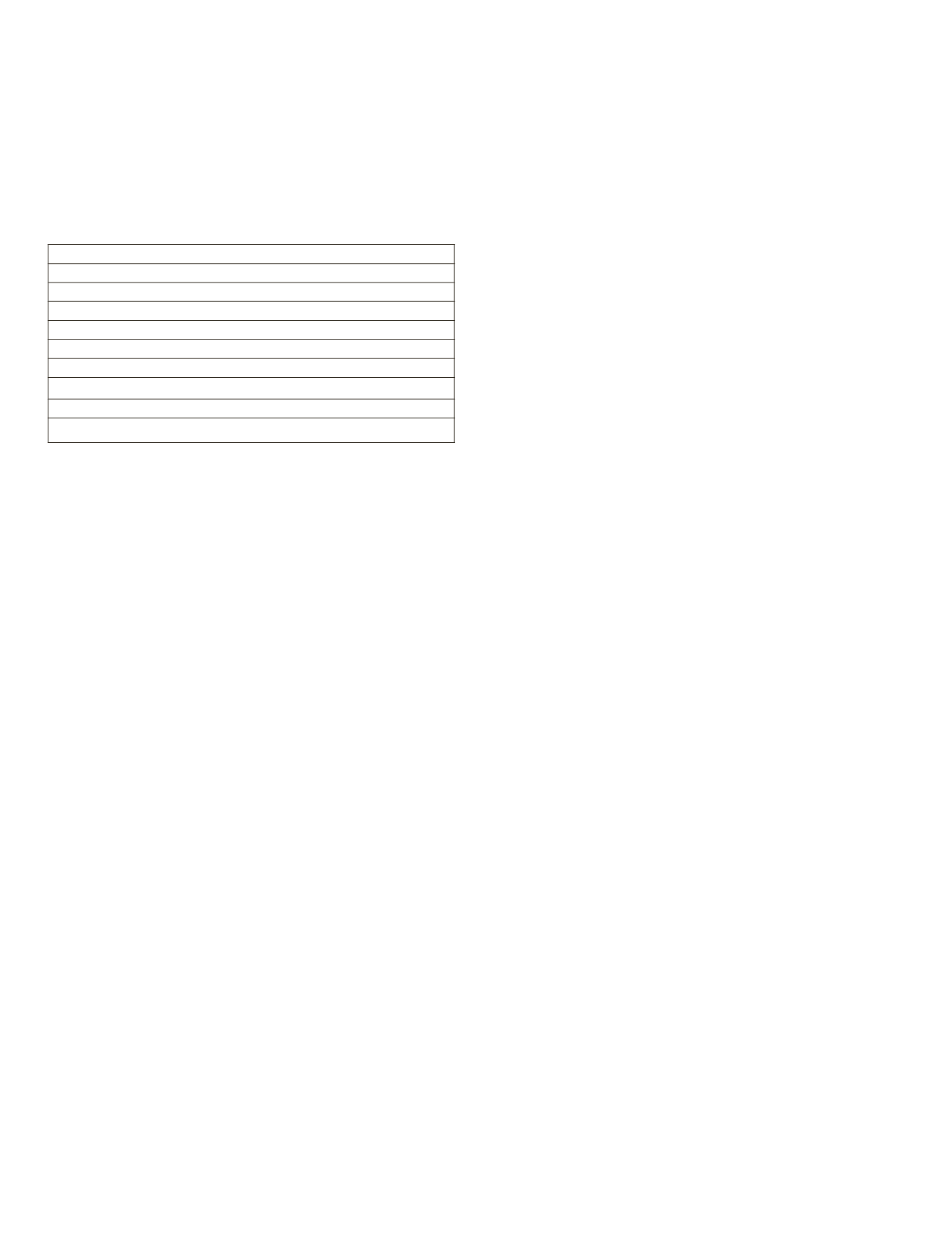
where |
S
| stands for the number of voxels included in the
segment
S
and
δ
denotes a constant parameter setting the
initial threshold value. In the extreme case, if
|S
m
|
= 1 and
|
S
n
|
= 1, then
τ
mn
=
δ
mn
. The merging process is carried out
repeatedly by traversing all the possible edges. In Algorithm
1, we provide a detailed description of the graph segmenta-
tion process. We assume the central voxel of a graph to belong
to the same segment as all neighboring voxels that were con-
nected to it in the graph segmentation procedure.
Algorithm 1: Efficient segmentation of the local graph
Input:
G
= (
V
,
E
), Local graph with vertices
V
and edges
E
Output:
C
= [S
1
, S
2
, ..., S
n
]: Segments of vertices
0: Sort
E
in ascending order according to its weight
w
1: Initial segmentation
C 0
= [
S
1
,
S
2
, ...,
S
m
],
S
i
= [
V
i
]
2: Initial threshold
τ
ij
=
δ
,
I
i
= 0
3: for
"
E
ij
∈
E do
4: If w
ij
>
τ
ij
= max(
I
i
+
δ
, I
j
+
δ
)
5:
S
k
Ü
S
i
È
S
j
6:
I
k
= w
ij
+
δ
||
S
i
|
S
j
|
7:
C
Ü
{
C
\{
S
i
È
S
j
}}
È
S
k
Clustering of Voxels
Once the connections of the voxels are identified, the voxels
are clustered into segments. This clustering process is per-
formed repeatedly by traversing all the voxels with a depth-
first search strategy. Connected voxels are aggregated into one
single segment. Additionally, a cross validation process is
required to examine the correctness of connections. In detail,
for adjacent
V
i
and
V
j
, after segmenting the graph of
V
i
, if
V
i
is identified as connected to
V
j
, then in the segmentation of
graph of
V
j
,
V
j
should be connected to
V
i
as well, and vice
versa. Otherwise, they are identified as disconnected.
SVGS: Super-Voxeland Graph-Based Segmentation
The
SVGS
method is an improved solution based on the
supervoxel structure and the local affinity graph, extended
from our prior work (Xu
et al.
, 2016). There are three signifi-
cant differences of the
SVGS
method compared with the
VGS
method. First, the basic element for segmentation is differ-
ent. In
SVGS
, supervoxels are applied for clustering segments
instead of voxels. Second, the construction of the local graph
is different. For the
SVGS
method, we use the local adjacency
graph for each supervoxel rather than the fully connected
graph used in
VGS
. Last, for clustering connected basic ele-
ments (i.e., supervoxels), the aggregation process is conducted
through the merging of adjacency graphs. The purpose of
using supervoxels is twofold: first, to improve the efficiency
of the proposed strategy, because the use of supervoxels can
largely reduce the number of basic elements used for segmen-
tation; furthermore, the construction and segmentation of the
local adjacency graph designed for supervoxels are simpler, so
that theoretically it also requires less computational resourc-
es. The second aspect concerns the ability of supervoxels to
preserve edges, as supervoxels have been proven to be quite
effective when finding over-segmented boundaries of objects.
Generation of Supervoxels
Supervoxels are generated using the Voxel Cloud Connectiv-
ity Segmentation method (
VCCS
) (Papon
et al.
, 2013), which
considers candidate voxels according to their distance to seed
points within a feature space comprising centroid positions,
normal vectors, geometrical features, and RGB colors. Some-
what different from the approach in (Papon
et al.
, 2013), we
calculate the distance using only normal vectors and spatial
coordinates of voxels, which is related to the proximity and
continuity laws of perceptual grouping. The variant of
VCCS
we used in
SVGS
is adopted from the Point Cloud Library
(
PCL
) (Rusu and Cousins, 2011). One of the most significant
advantages of
VCCS
is its ability to preserve boundaries (Papon
et al.
, 2013), through which we can obtain supervoxels the
boundaries of which coincide with the boundaries of major
structures of objects in the scene. It is also notable that the
size of voxels (i.e., the resolution of the voxel structure) and
the resolution of seeds can greatly affect the performance of
VCCS
. To be specific, the former determines details preserved
in the segments, whereas the latter influences the effective-
ness of retaining boundaries. Empirically, we set these factors
according to point densities and varying distances from the
sensor to objects within the scene.
Local Adjacency Graph of Supervoxels
Unlike fully connected local graphs used in
VGS
, to apply the
graph model to the supervoxel structure, we define a local
adjacency graph for each supervoxel encoding all its adjacent
supervoxels in a local neighborhood. This is due to the fact
that the generation of supervoxels already encapsulated the
geometric information of voxels into the supervoxel, so that
supervoxels have become independent units. Thus, there is no
need to construct a fully connected graph for each supervoxel.
Besides, the use of the local adjacency graph can also help to
reduce the computational cost. Specifically, for each super-
voxel
V
i
, all its
n
adjacent neighbors are counted as candidates
for constructing the contextual graph
G
i
= {
V
,
E
}, which is
represented in the form of nodes. Here,
V
and
E
represent the
sets of all the supervoxels (i.e., nodes) and edges in the graph,
respectively. A spherical neighborhood defined by radius
R
c
is
defined as the local context of each supervoxel. Any super-
voxel with its centroid located inside this spherical neighbor-
hood will be regarded as a candidate of a direct neighbor of
the center supervoxel. Then, the distance between the centroid
of the candidate supervoxel and the centroid of the center su-
pervoxel is measured. If this distance is smaller than
√
3
ι
, this
candidate supervoxel will be regarded as an adjacent super-
voxel of the center supervoxel. Here,
ι
is the seed resolution
defining the size of supervoxels when using
VCCS
. We use a
kd-tree to conduct the nearest neighbor search. The weights of
the edges E are determined using the same measures based on
the laws of perceptual grouping as in the case of
VGS
. Here, the
attributes of supervoxels are calculated using points inside all
voxels of the supervoxel. The partition of the local adjacency
graph
G
is also carried out in a similar fashion as for
VGS
, using
graph-based segmentation (Felzenszwalb and Huttenlocher,
2004), by which the segmented graph
G*
can be obtained. The
supervoxel assigned to the central supervoxel according to
G*
are considered to be connected to that supervoxel.
Aggregation of Supervoxels
After the partition of local adjacency graphs, to aggregate
supervoxels, all the segmented local adjacency graphs are
traversed and checked. Figure 5 shows an example, where the
node
V
k
is shared by graphs
G
i
*
and
G
j
*). Segmented graphs
sharing such common nodes will be merged into a large graph
G
representing a segment. At the end of this merging process,
each merged graph
G
will correspond to a segment. Similarly,
during the identification of connections for each supervoxel,
the cross validation used in
VGS
is also conducted. In Figure
5, we give an illustration of how the local adjacency graphs
are constructed, partitioned, and aggregated.
Experiments
Experimental Datasets
For testing the performance of the proposed strategy, we
conducted experiments using point clouds acquired from two
382
June 2018
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING