D
c
ij
= (
α
i
−
α
j
)
2
+ (
π
−
α
i
−
α
j
)
2
if
α
i
−
α
j
≤
θ
(2)
(
α
i
−
α
j
)
2
+
π
2
else
For the case of surfaces with a smooth local configuration
(see Figure 3a), the angles
α
i
and
α
j
are both around
π
, the
value of continuity is almost zero. In contrast, for the case
of surfaces with a “stair-like” local configuration (see Figure
3b), the surfaces are highly likely to be separated parts of
different objects and should be split. If the angles
α
i
and
α
j
are both around
π
+
φ
, the value of continuity is around 4
φ
2
.
Whether the “stair-like” surfaces should be disconnected or
not depends on the value
φ
. For the cases of surfaces with a
convex or concave local configuration, similar to the work
reported in (Stein
et al.
, 2014), for one object, it is assumed
that the surfaces with a convex connection should always be
preserved while the ones with a concave connection should
be split according to the degree-of-convexity criterion.
For instance, assuming that the angle
α
i
=
π
2
+
∈
and the
angle
α
j
=
∈
in Figure 3c, the value of continuity is around .
In contrast, if the angles
α
i
=
∈
and
α
j
=
π
+
∈
in Figure 3d, the
value of continuity is around . It is clear that the continuity
measure of the surfaces with a convex local configuration is
much smaller than that of the surfaces with a concave local
configuration, although the absolute values of the angle differ-
ences
∈
are the same.
Local Graph-Based Clustering
In classical methods, the connectivity of voxels is identified by
information extracted from merely two adjacent voxels, based
on their similarity or on normal vectors (Wang and Tseng,
2011; Papon
et al.
, 2013), but due to the complexity of 3D
scenes, the assessment of connections considering only pair-
wise information seems unreliable. Therefore, we utilize the
graph theory to estimate the connections of each voxel, consid-
ering information of all the adjacent voxels in a given neighbor-
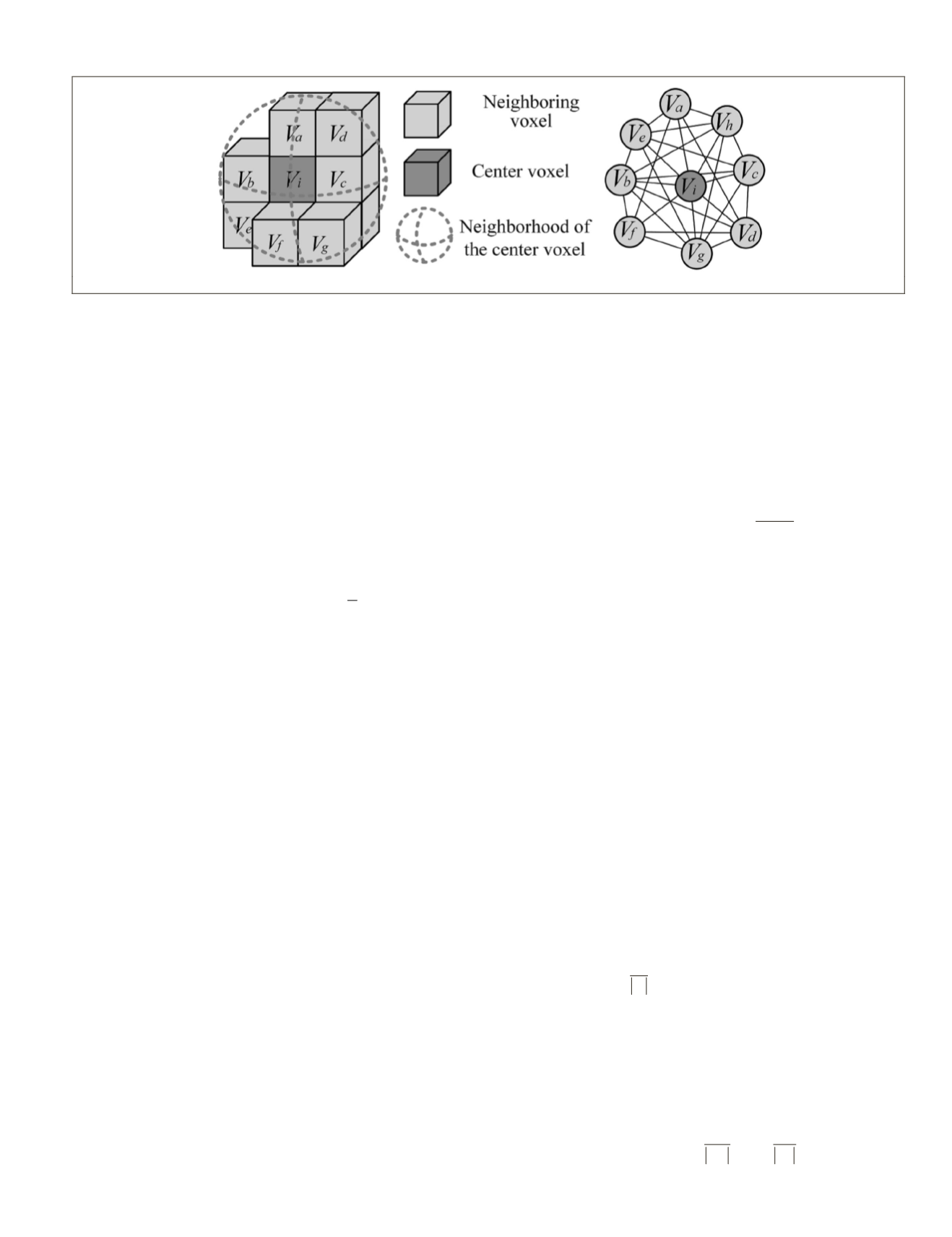
hood of a central voxel simultaneously. Here, a fully connected
local graph
G
= (
V
,
E
) is proposed as shown in Figure 4.
Fully Connected Local Graph of Voxels
Graphical models have been widely used in many point cloud
segmentation tasks. By using graphical models, the connectiv-
ity of two adjacent patches can be assessed in a context-aware
way. The majority of approaches using graphical models
operate at a global scale, i.e., they construct a graph for the
entire scene and each point or element is related to a node
(i.e., points or patches) of the graph (Golovinskiy and Funk-
houser, 2009; Pham
et al.
, 2016b). However, a large graph will
significantly increase computational costs of the construc-
tion and partitioning steps. To avoid this problem, we define
a local contextual graph for each voxel considering all the
neighboring voxels in a local neighborhood. It means that the
size of the constructed graph is limited to the neighborhood
of the central voxel. The nodes in the graph correspond to
the central voxel and its adjacent neighbors. In
VGS
, the local
contextual graph is fully connected, which ensures optimal
extraction of geometric information in the neighborhood. For
the fully connected local graph, voxels are regarded as verti-
ces
V
while the edges
E
link all the possible pairs of vertices.
For each voxel, all adjacent voxels in its local graph that are
connected to it according to the local graph segmentation
procedure are considered to belong to the same segment. The
weight
w
ij
∈
[0, 1] between
V
i
and
V
j
is defined by joining all
the
D
k
ij
,
k
∈
[
p
,
s
,
c
] between voxels by multiplication, because
they are assumed to be independent:
w
D
ij
k p s c
ij
k
=
−
(
)
∈
[
]
∏
, ,
exp
λ
κ
2
2
(3)
where
λ
p
,
λ
s
, and
λ
c
are parameters controlling the importance
of the spatial distance, the geometric similarity, and the sur-
face continuity, respectively.
Efficient Graph-Based Segmentation
Once the local graphs of all voxels are constructed, we can
estimate the connections of each voxel by partitioning the
constructed local graph. To this end, an efficient graph-based
segmentation method is introduced by adapting the algorithm
proposed in (Felzenszwalb and Huttenlocher, 2004). Here, the
segmentation
C
partitions vertices
V
(i.e., voxels) into seg-
ments
S
∈
C
corresponding to connected components in the
graph. Initially, every vertex
V
i
is deemed to be one segment
S
i
. The edges are sorted in ascending order by their weights.
Afterwards, the graph is partitioned using an iterative process
by comparing the maximum internal difference
I
i
inside a seg-
ment
S
i
and the external difference between segments
S
i
and
S
j
. Here, the maximum internal difference of a segment relates
to the largest weight of the edges between vertices included in
the segment. In contrast, the external difference is the mini-
mum weight of the edges connecting two voxels of different
segments in the graph. If the maximum internal difference of
one segment is larger than the external difference between
this segment and another segment, we will merge these two
segments. After the merging of two segments, the maximum
internal difference
I
of the new segment is updated, and it is
increased by a term
δ
S
ij
associated with the number of voxels
in the newly merged segment. Specifically, for vertices
V
i
∈
S
m
and
V
j
∈
S
n
of an edge
E
ij
,
S
m
and
S
n
will be merged, if
E
ij
has
the smallest weight of all the possible edges connecting verti-
ces of different segments
S
m
and
S
n
and the weight
w
ij
of
E
ij
is
larger than the threshold
τ
mn
. Here, the weight
w
ij
is related to
the external difference between
S
m
and
S
n
. The threshold
τ
mn
is estimated as follows:
τ
δ
δ
mn
m
m
n
n
I
S
I
S
=
+
+
max
,
(4)
Figure 4. Constructing the local graph of a voxel: (a) Adjacent voxels in a neighborhood, and (b) Fully connected local graph.
PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
June 2018
381


