PHOTOGRAMMETRIC ENGINEERING & REMOTE SENSING
March 2018
127
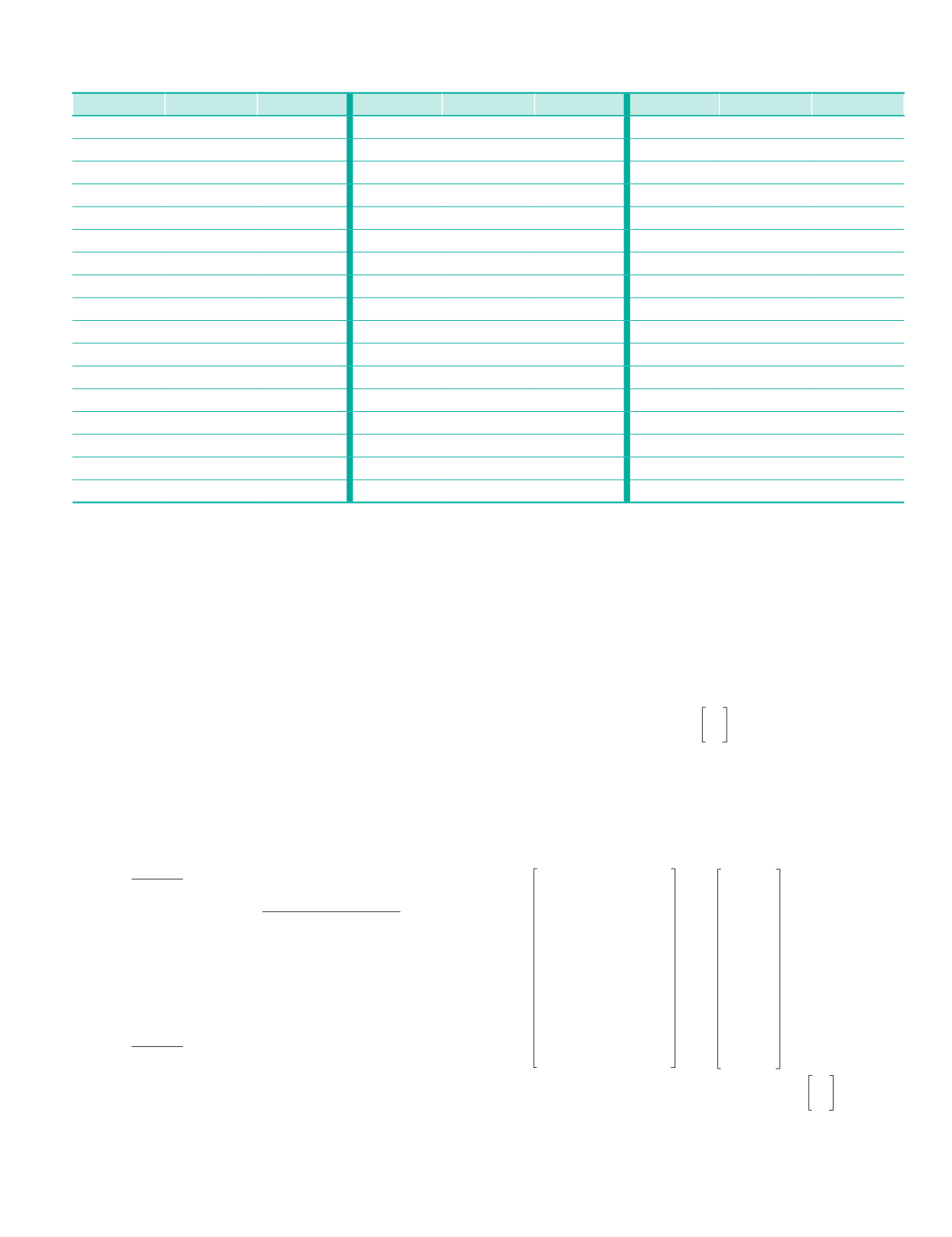
Table A1: Lists 50 nearest neighbors for the point chosen (931210.58, 843357.87 and 15.86) in swath # 1.
X
Y
Z
X
Y
Z
X
Y
Z
931211.7
843357.7
15.9
931213.5
843358.4
15.97
931212.6
843361.5
16
931211.7
843358.1
15.94
931212.5
843360.1
15.94
931211.7
843362
16
931211.6
843358.7
15.94
931212.7
843355.7
15.9
931214.7
843359.1
15.81
931212.2
843357.7
15.81
931213.4
843358.9
15.9
931214.3
843360.1
15.94
931211.8
843356.6
15.81
931213.1
843360.1
15.9
931214.8
843356.5
15.81
931212.8
843357.7
15.81
931214
843357.7
15.84
931213.5
843361.3
16
931212.4
843356.5
15.74
931214.1
843358.4
15.97
931212.3
843362.1
16
931212.9
843358.3
15.84
931211.6
843361.3
15.97
931213.2
843361.6
16.07
931211.9
843360.1
16
931214
843359
15.84
931215.3
843357.7
15.84
931213
843356.5
15.77
931212.2
843361.3
15.87
931215.2
843358.6
15.9
931213.4
843357.7
15.84
931213.7
843360.1
15.9
931214.9
843360
15.9
931214.7
843361.3
15.94
931214.2
843356.5
15.77
931215.2
843359.1
15.97
931215.5
843360
15.87
931212
843361.4
16.07
931212.9
843362.1
16.07
931214.4
843361.7
15.97
931214.6
843357.7
15.81
931214
843361.3
15.94
931215.9
843359.2
15.9
931212.9
843361.3
16
931215.4
843356.5
15.81
931212.2
843352.6
15.94
931214.7
843358.5
15.9
931215.8
843358.6
15.94
931214.7
843354.2
15.77
931215.9
843357.7
15.81
2000-5000 DQM measurements depending on the size of the
swaths can be made and recorded per pair of overlapping
swaths.
Error Analysis
Once the outputs file (A portion of an example output file is
shown in Table A2) is generated, the file may be analyzed to
determine vertical and horizontal errors in the data. The first
analysis step is to divide the output file into two sets of mea-
surements, based on the arc cosine of the Nz column.
arc cosine
(
Nz
)
i
>10 degrees, Measurement is in Sloping terrain
≤5 degrees, Measurement is in flat terrain
{
Vertical Error
The vertical error can be determined by the ‘D’ column of all
measurements from the flat terrain:
Δ
Z
average
∑
i
=1
D
i
Nf
Nf
, where Nf is the number of measurements
found on flat terrain and σ
z =
∑
i
=1
(
D
i
–Δ
Z
average
)
2
Nf
Nf
–1
.
In the data shown in Table 1, the vertical errors are calcu-
lated using the values in the first 10 rows (i.e. having slopes
less the 5 degrees as defined by arc cosine of the Nz column).
For this example, the vertical error and the corresponding
standard deviation are calculated as:
Δ
Z
average
∑
i
=1
D
i
10
10
= 0.041m and the standard deviation as
0.131 m, with a root mean square error (RMSEz) of 0.131 m.
Horizontal Error
The horizontal error is determined from measurements made
from sloping terrain. It is suggested that at least 30 such
measurements are available; otherwise the values may not be
valid. In the example shown, for the sake of clarity, only 10
DQM measurements (as shown in Table 2) are used.
To determine horizontal error, generate a matrix as shown
below:
N =
[
N
x
N
y
]
Measurements from sloping terrain only
Calculate
D
r
= D
–
N
z
× ∆Z
average
for all measurements from
sloping terrain and solve
N ×
∆
X
∆
Y
=
D
r
to obtain estimates of
horizontal errors represented by ∆
X
and ∆
Y
(as well as esti-
mates of their standard deviation). There are several least
squares open source solvers available in all languages which
can be used to obtain the estimates.
In this case, the values of N and
D
r
are:
N
=
0.0267 0.2176
0.0541 – 0.1723
0.0589 0.2005
0.0730 0.1749
– 0.0710 – 0.2039
0.1627 0.1049
0.0718 0.1823
0.2055 0.0939
0.0766 0.1711
0.1350 0.1832
,
D
r
=
– 0.314
0.448
– 0.315
– 0.232
0.364
0.082
– 0.197
0.139
– 0.375
– 0.395
Using Least Squares, the solution to solve
N ×
∆
X
∆
Y
=
D
r
is ∆
X
= 1.43m and ∆
Y
= – 2.21m. Note that if these numbers seem
excessively high, an illustration of the horizontal errors for
this data is shown in Figure A2.


